Simulación matemática de la degradación del kerógeno y generación de hidrocarburos en el pozo exploratorio IRME-1: caso a temperatura constante
1Alberto Hernández Rosales, 1Diana Margarita Garza Cavazos, 1Karla Rosalyne Lira Méndez, 1Roberto Díaz Martínez, 1Felipe de Jesús López Saucedo.
Resumen
En el presente trabajo de investigación, se hace una simulación matemática de la degradación del kerógeno y generación de hidrocarburos a temperatura constante. En dicha simulación se estiman los límites de producción de x, y, u1 y u2 (kerógeno, compuestos heteroatómicos pesados, hidrocarburos, resinas y asfaltenos) usando un modelo matemático, con muestras obtenidas del pozo exploratorio IRME-1 de la zona de la cuenca de Sabinas, Coahuila México; con el objeto de conocer una aproximación cuantitativa de la cantidad de subproductos producidos en la zona; además de una estimación gráfica de los límites de producción de x,y,u1 y u2.
Palabras clave: kerógeno, modelo matemático, límites, producción, simulación.
Abstract
In the current research work, a mathematical simulation is done, of Kerogen degradation and generation of hydrocarbons at a constant temperature. In this representation the production limits of x, y, u1 y u2 are estimated. (kerogen, heavy heteroatomic compounds, hydrocarbons, resins and asphaltenes) using a mathematical model, with samples taken from the IRME-1 exploratory well in the Sabinas, Coahuila Mexico basin area. In order to know a quantitative approximation of the quantity of by-products produced in the area; in addition to a graphic estimate of production limits of x,y,u1 and u2.
Keywords: kerogen, mathematical model, limits, production, simulation.
Introducción
Al noreste de México, en el estado de Coahuila de Zaragoza, se localiza la Cuenca de Sabinas, la cual se ha comenzado a estudiar para la extracción del gas shale. Como el petróleo y gas natural son resultado de la degradación del kerógeno, es aquí donde entra la necesidad de contar con un estudio de la historia de una cuenca sedimentaria. Modelos matemáticos basados en la cinética de la degradación del kerógeno, y usando simulación por computadora se obtiene una aproximación cuantitativa. El trabajo consiste en expresar adecuadamente la formación del petróleo y gas como una función del tiempo (Tissot y Welte, 1984).
Esta investigación entra en la categoría de estudios exploratorios y consiste en el estudio del pozo IRME-1, ubicado en la subcuenca de Sabinas; se pretende estudiar y analizar las simulaciones a través del modelo matemático, propuesto por (Tissot, 2003); obteniéndose la producción de hidrocarburos, resinas y asfaltenos, a temperatura constante con la ayuda de los parámetros cinéticos (Ea,A), obtenidos de las 21 muestras del pozo IRME-1.
Marco geológico
En Coahuila se reconoce la Cuenca de Sabinas en la región central. Geológicamente, la Cuenca de Sabinas está constituida por ocho subcuencas que se corresponden con sinclinales amplios, cuya orientación NW-SE se ajustan a la estructura regional. Estas subcuencas se designan como Sabinas, Esperanzas, Saltillito, Lampocitos, San Patricio, Las Adjuntas, Monclova y San Salvador (Corona et al. 2006), de las cuales, la Cuenca de Sabinas es la más importante por su extensión y contenido de carbón (SGM (a), 2008).
Durante el Cretácico Superior (Cenomaniano Superior-Turoniano) se depositó la Formación Eagle Ford. Esta se encuentra ampliamente distribuida en el noreste de México, en la superficie y el subsuelo de la Cuenca de Sabinas y en los bordes de la Península de Tamaulipas, así como en el borde noreste de la Cuenca de Burgos (SMG (b), 2008).
La Formación Eagle Ford está constituida por lutitas calcáreo-carbonosas laminares de color gris oscuro a negro. Su espesor promedio es de 100 a 150 m, pero ha llegado a medir 320 m (SGM (b), 2008). Ésta se depositó en un ambiente de sistema transgresivo, en un ambiente nerítico medio (SGM, 2006), lo que explica la predominancia de rocas de sedimentos finos (lutitas), con alto nivel de materia orgánica, clasificada como Tipo II y predominantemente Tipo III (Camacho, 2009).
En la Provincia Petrolera Sabinas-Burro-Picachos, a la cual pertenece nuestra área de estudio, se han identificado tres sistemas petroleros, relacionados con rocas generadoras del Tithoniano, Aptiano y Turoniano. Estos sistemas petroleros productores de gas y condensado, se distribuyen ampliamente en dicha cuenca. Las características geoquímicas del contenido orgánico y sobremadurez definen las rocas del Tithoniano como la principal roca generadora de esta provincia petrolera que es clasificada como conocida (!). Se han identificado otras rocas generadoras de edad Aptiano y Turoniano, sin precisar su participación con los yacimientos (PEMEX, 2013).
En el sistema petrolero Turoniano-Turoniano, la roca generadora está representada por lutitas y calizas arcillosas depositadas de la Formación Eagle Ford del Turoniano en un ambiente de plataforma externa, con espesores netos de 28 a 300 m y valores de TOC que van de (0.6%) hasta excedente (5.0%) (PEMEX, 2013). La madurez reportada se presenta en el rango de inmaduro (0.2%) hasta de sobremaduro (> 1.2%) hacia las áreas de Monclova y Nuevo Laredo. El kerógeno observado para este subsistema es de Tipo II y III, precursor de aceite y gas (PEMEX, 2013).
Análisis Rockeval
Existen diferentes métodos para la obtención de los parámetros cinéticos requeridos para conocer la cinética del kerógeno de la zona de estudio. En esta investigación usamos la técnica de pirólisis Rock-Eval 6 debido a su rapidez y confiabilidad (Behar et al., 2001).
Esta técnica usa temperaturas de calentamiento programadas para una pequeña cantidad de roca o carbón en una atmósfera inerte (helio o nitrógeno) con el fin de determinar la cantidad de hidrocarburos libres presentes en la muestra (pico S1) y aquellos que pueden potencialmente ser liberados después de la maduración (pico S2). El valor de Tmax es un parámetro estandarizado calculado de la temperatura a la cual el pico S2 alcanza su máximo. Estos parámetros describen la cantidad de materia orgánica en la muestra de roca para propósito de exploración (Behar et al. 2001).
Las muestras típicamente rondan de 50 a 70 mg de roca, de 10 a 30 mg de carbón y de 5 a 15 mg en el caso de la materia orgánica aislada. Sin embargo, por el alto potencial petrolero como es el caso del Tipo I, las muestras pueden ser reducidas hasta 1-2 mg (Behar et al. 2001).
Parte experimental
Las muestras utilizadas para la simulación matemática de la degradación del kerógeno y generación de hidrocarburos fueron obtenidas mediante una campaña de perforación a cargo de la Escuela Superior de Ingeniería “Licenciado Adolfo López Mateos”, del pozo exploratorio IRME-1 con las coordenadas UTM 294322E, 3102055N ubicado en el rancho “La Esperanza”, en el municipio de Sabinas Coahuila, vease la (Véase Figura 1); el cual abarcó núcleos desde los primeros 22.52 m a los 162.8 m de profundidad, perforando la parte inferior de la formación Austin, La totalidad de la Formación Eagle Ford y la parte superior de la Formación Buda.
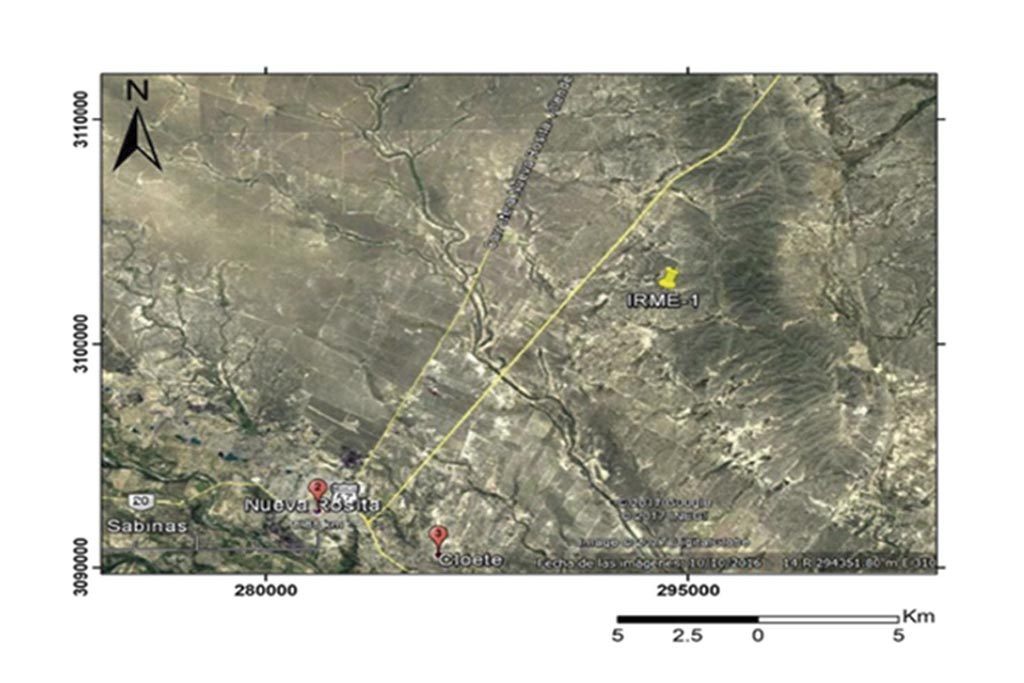
Figura 1: Ubicación geográfica del pozo IRME-1. Fuente Google Earth.
De dicho pozo se recuperaron las muestras utilizadas en esta investigación, pertenecientes a la Formación Eagle Ford, siendo recuperadas un total de 21 muestras, 18 fueron de lutita bituminosa, a las que se les aplicó análisis Rock-Eval, con los resultados de éste, se hizo un procesamiento de los datos mediante el software Geoworks para la obtención de la distribución de las energías de activación y factor de frecuencia de las muestras, lo que serviría posteriormente para el conjunto de simulaciones requeridas.
Modelo matemático de la degradación del kerógeno y generación de hidrocarburos.
El modelo matemático de generación de hidrocarburos fue introducido por (Tissot, 1969) y es discutido en (Tissot y Espitalie, 1975). El modelo matemático usa un esquema general de la evolución del kerógeno, véase (Tissot et al. 1978).
Los modelos cinéticos de la degradación del kerógeno se presentan a través de la cinética química de las reacciones de primer orden, A⟹B+C, donde A es el único reactivo y B,C son los productos (Goncalves et al. 2001).
Para simular el sistema de reacciones, que se muestran en la Figura 2, se hace mediante el siguiente esquema: A, B1,…,Bn-1, Bn, esto fue propuesto por Tissot (1969), lo cual parece ser suficiente para explicar la formación sucesiva de aceite y gas (Tissot y Espitalie, 1975).
A continuación, damos la última formulación dada en (Tissot, 2003), véase la Figura 3. En este caso A representa el kerógeno, compuesto de ni enlaces de tipo i, en un tiempo t; xi es la cantidad de materia orgánica reaccionando en la ith reacción; yi y uj representan la cantidad de compuestos Bi y Cj respectivamente.
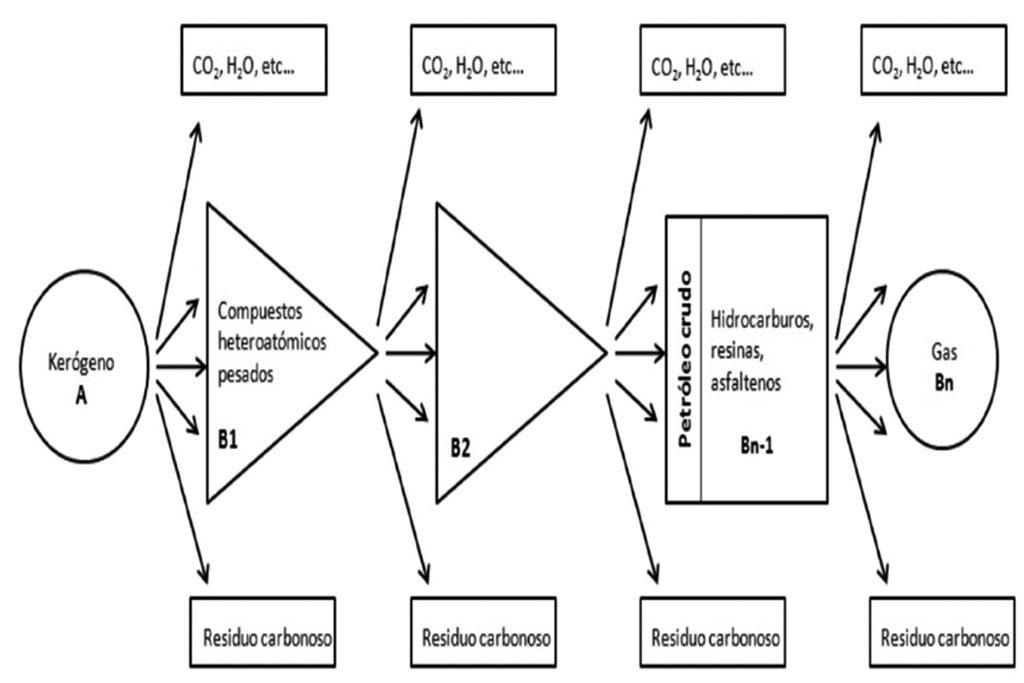
Figura 2: Marco general de la degradación del kerógeno (Tissot 1969).
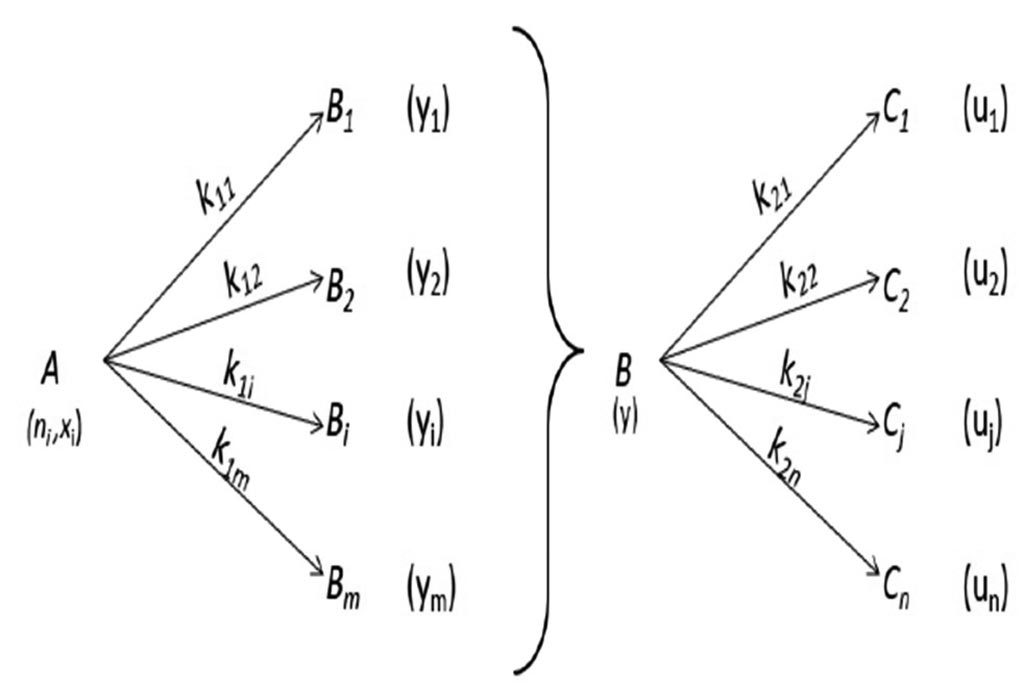
La cantidad de kerógeno es representada por x y y representa la cantidad de compuestos heteroatómicos pesados, u1 y u2 representan hidrocarburos aromáticos, resinas y asfaltenos, respectivamente.
En estas reacciones, la disminución relativa de la cantidad de reactivo es directamente proporcional al tiempo en que ocurre la reacción, esto es expresado por la relación: -dx=kdt, donde x es la concentración de reactivo (kerógeno), k es la constante de tasa y t es el tiempo (Goncalves et al. 2001). La tasa de conversión v del reactivo en los productos también es proporcional a su concentración: (Goncalves et al. 2001).
Por su parte, la constante de tasa k es función de la temperatura, conforme lo expresa la ley de Arrhenius: , donde E1i es la energía de activación de la ith reacción, A1i es la constante factor de frecuencia, T temperatura absoluta y R la constante universal de los gases (Peters et al. 2006) y (Goncalves et al. 2001). El factor de frecuencia representa la frecuencia de choques entre las moléculas mientras la energía de activación puede ser comprendida como el umbral de energía por encima del cual las reacciones químicas comienzan. Estas dos variables o parámetros (factor de frecuencia y energía de activación) son comúnmente conocidas como parámetros cinéticos y son características de cada reacción.
Las cantidades xi,yi y uj pueden ser obtenidos del siguiente sistema de ecuaciones diferenciales de primer orden, véase (Tissot et al. 1978).
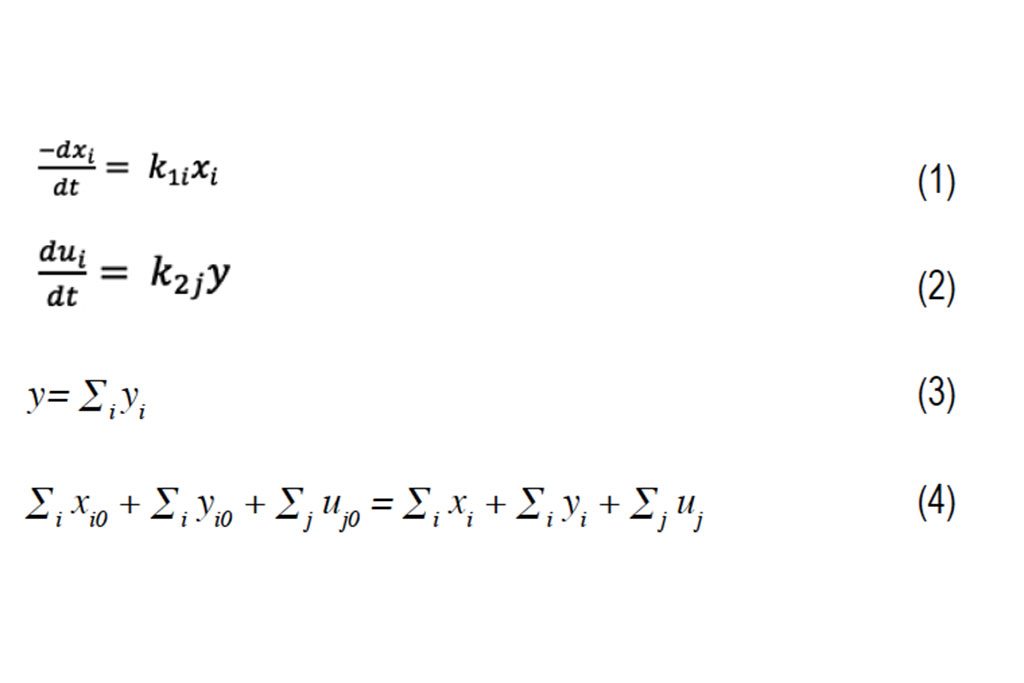
donde las dos primeras ecuaciones expresan las cinéticas del sistema y las dos últimas el balance de masa.
Estudio teórico de la cinética del kerógeno y generación de hidrocarburos a temperatura constante
Consideremos el diagrama propuesto por Tissot (2003), véase la Figura 4.
Se hace el siguiente análisis de la cinética del kerógeno y generación de hidrocarburos a temperatura constante con el objetivo de aplicar posteriormente esta idea a las muestras del pozo IRME-1 ubicadas en la Cuenca de Sabinas.
Realizamos el análisis del sistema de ecuaciones considerando enlaces de un tipo (i), a una frecuencia Pi=1, y la reacción de B a C de dos tipos.
Por lo tanto, el sistema de ecuaciones anterior es el siguiente, véase (Tissot et al. 1978), y Tissot (2003).
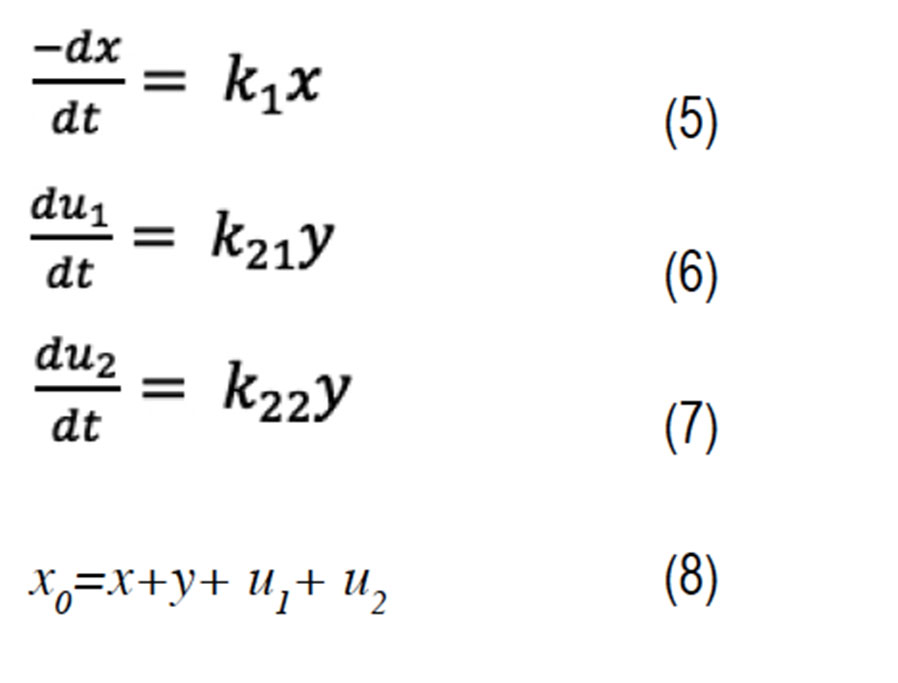
Según Tissot (2003), se consideran los valores de y0=u10=u20=0 debido a que en el estado inicial el kerógeno aun no produce ningún hidrocarburo.
Haciendo algunos cálculos, se obtienen las siguientes expresiones matemáticas, véase (Tissot, 2003):
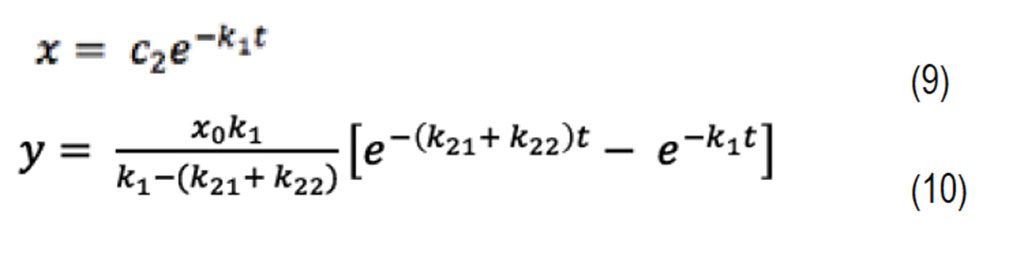
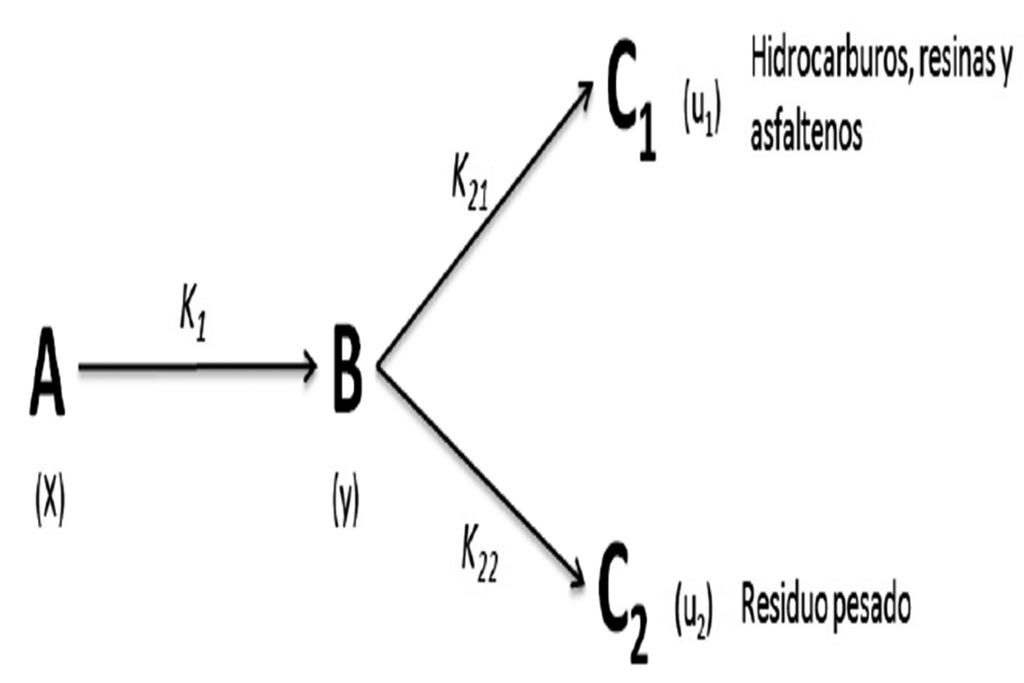
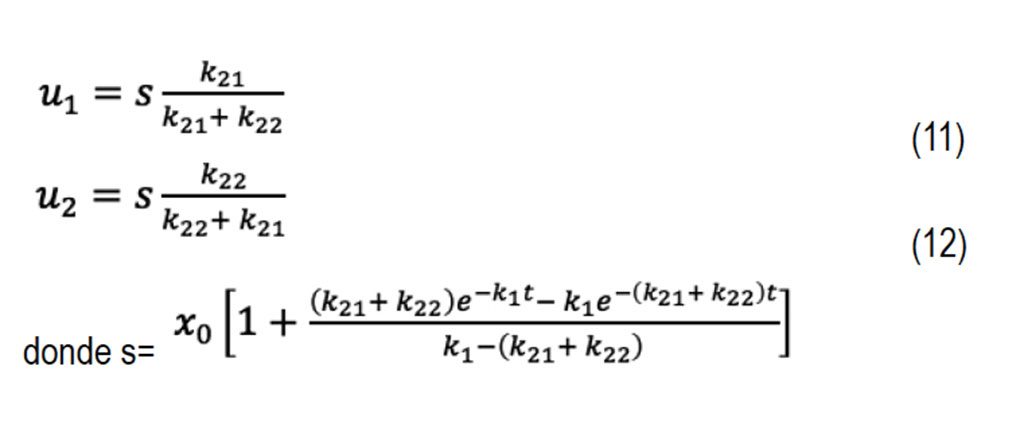
Por otro lado, si suponemos que en el instante de tiempo t=0 reaccionó una cantidad x0 de materia orgánica labil ( x(0)= x0 ), entonces tenemos lo siguiente:
límt→∞ xi (t)= límt→∞ x0 e-k1t=0, es decir, la materia x (kerógeno) se degrada para transformarse en hidrocarburo. Del mismo modo para las Ecuaciones (10), (11) y (12), tenemos:
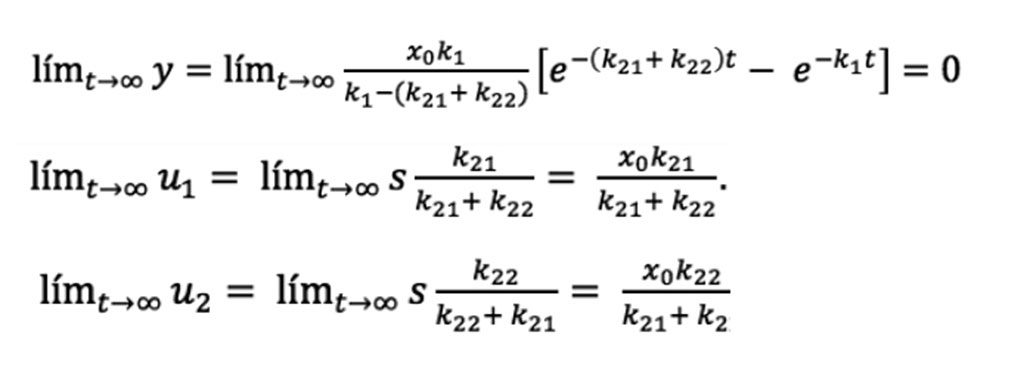
Tomando en cuenta que u1 y u2 dependen directamente del tiempo. Hacemos un análisis de diferentes casos para los valores de k.
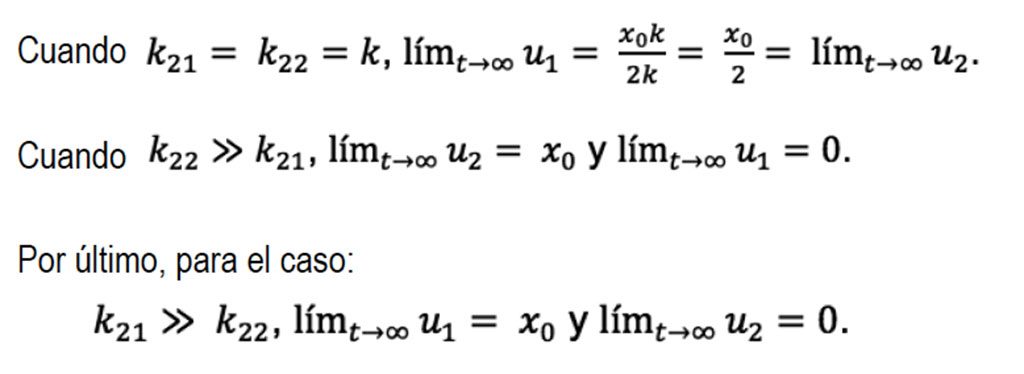
Simulación del pozo exploratorio IRME-1
Para la simulación a temperatura constante, se utilizaron los datos recabados mediante análisis Rock Eval de 21 muestras de la Formación Eagle Ford; estos fueron analizados con el software Geoworks, para obtener un histograma de las energías de activación de cada muestra, así como el factor de frecuencia para todas las muestras. Las energías de activación que se utilizaron para las simulaciones, así como el factor de frecuencia se presentan en la Tabla 1, donde se utilizó el primer valor del intervalo del histograma para el cálculo del parámetro k11, el primer valor del intervalo en el que se generaron más hidrocarburos para el k21 y para el cálculo del k22 el primer valor del intervalo con las energías de activación más altas presentes en las muestras. El factor de frecuencia que se usa en todas las simulaciones es 1X1013.
Energias de activación en las simulaciones
| k1 | k21 | k22 |
| Ea más baja (Kcal/mol) | Ea con mayor generación de hidrocarburos (kcal/mol) | Ea más alta (kcal/mol) |
| 41 | 51 | 59 |
Tabla 1. Energías de Activación usadas en la simulación del caso real. (Ea: energía de activación; k1,k21 y k22: parámetros resultantes a temperatura constante).
En la obtención de las paleotemperaturas necesarias para el modelo, se utilizaron los valores de la reflectancia de vitrinita máximos y mínimos registrados para la Formación Eagle Ford por Camacho Ortegón (2009), teniendo los valores 0.8 y 1.29; además del valor de 1.35, extraído de Resendiz (2017) para la misma formación. Utilizando la ecuación de Baker dada en Mark y David (1996), se hizo la conversión de la reflectancia de la vitrinita a temperatura en grados centígrados (ºC), obteniéndose los valores presentados en la Tabla 2.
Para el caso del tiempo, tenemos que la Formación Eagle Ford inicia su formación durante Cenomaniense (Cretácico Superior), por lo que de esa edad hasta la actualidad han transcurrido 100.5 millones de años; sin embargo, para proyectar su comportamiento en un futuro, en el modelo se le da un valor de 300 millones de años.
Con el fin de abarcar diferentes escenarios se hicieron tres simulaciones a temperatura constante, usando las mismas energías de activación y factor de frecuencia, sólo variando la paleotemperatura en cada caso.
| R0 (%) | Paleotemperatura (ºC) |
| 0.8 | 125 |
| 1.29 | 174 |
| 1.35 | 179 |
Tabla 2. Paleotemperaturas usadas en la simulación del caso real basadas en la reflectancia de la vitrinita (%Ro). T=104(ln Ro)+148, (Johnsson y Howell, 1996).
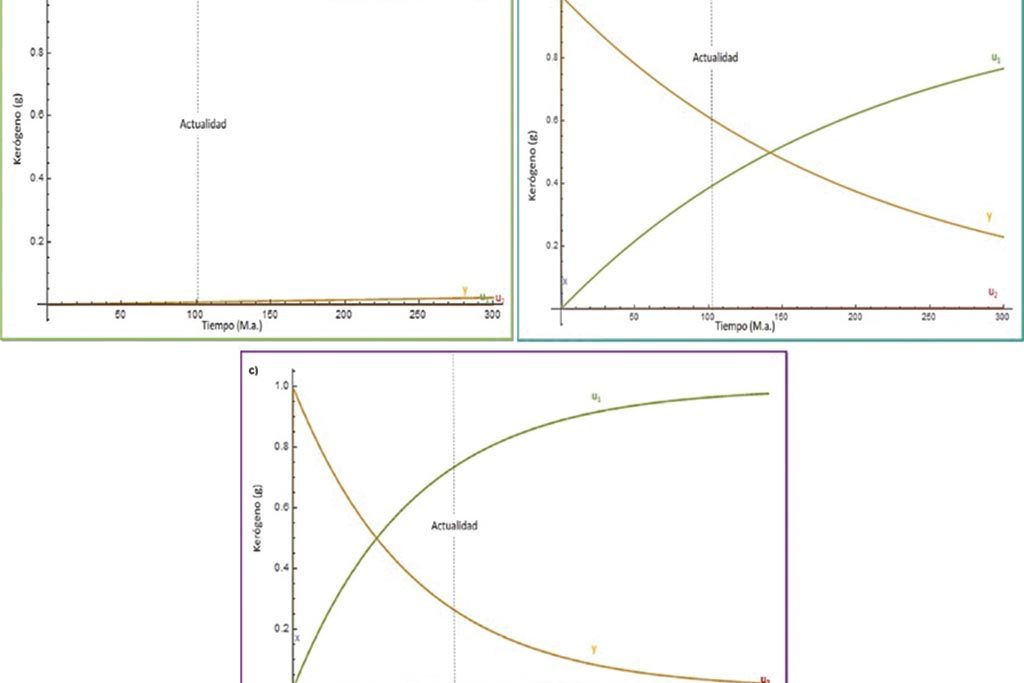
bajas y temperatura de 174 oC, c): Simulación 3 del pozo IRME-1 a temperatura constante:
caso Ea bajas y temperatura de 179 oC. (x= kerógeno, y= compuestos heteroatómicos
pesados, u1= hidrobarbueros, resinas y asfaltenos; u2= residuo pesado).
Para la Simulación 1, Figura 5 a), se utilizó una temperatura de 125°C. En este caso no se produjo degradación del kerógeno considerable (x; línea azul), éste se mantiene en el valor de uno sin una degradación visible, hasta después de los 100 M. a., donde comienza la formación de compuestos heteroatómicos pesados (y; línea amarilla), sin embargo, estos permanecen en valores muy bajos, mientras que los hidrocarburos, resinas y asfaltenos (u1; línea verde), y los residuos pesados (u2; línea roja) se mantienen casi en cero. Lo que refleja que para estas energías de activación, es necesario una mayor temperatura para la producción de hidrocarburos (u1).
Para la Simulación 2, Figura 5 b), se usó una temperatura de 174°C. Aquí se aprecia que con el aumento de la temperatura se propició la formación de subproductos. Al inicio el kerógeno (x; línea azul) se degrada rápidamente, al tiempo que comienza la formación de los compuestos (y; línea naranja), hasta llegar casi a la unidad en un tiempo menor a 10 M.a. para después comenzar a degradarse, a la par del paulatino aumento de u1 (hidrocarburos, resinas y asfaltenos; línea verde), el cual es formado a partir de y. A los 100.5 millones de años (que corresponde a lo que tenemos actualmente), vemos que tenemos una considerable formación de hidrocarburos u1, alrededor del 40% pero aún con una predominancia de compuestos heteroatómicos pesados y, lo que significaría que aún tenemos un gran potencial de generación.
Para la Simulación 3, Figura 5 c), usamos una temperatura de 179°C y se observa un aumento considerable en los hidrocarburos, resinas y asfaltenos, como se esperaba con el aumento de la temperatura, el cual propició las condiciones necesarias (mayor energía), para la formación aún más rápida de y y u1, a la par de una degradación casi instantánea del kerógeno x. Igualmente podemos ver una clara tendencia inversa en el comportamiento de y y u1, en el cual a medida que pasa el tiempo y disminuye, mientras que u1 aumenta; esto es debido a que los hidrocarburos, resinas y asfaltenos u1, se forman a partir de los compuestos heteroatómicos pesados y, los cuales al degradarse dan lugar a su formación, lo cual implica que a medida que y se degrada, da lugar a formación de u1.
Conclusiones
El modelo matemático usado en este trabajo de investigación para las simulaciones a temperatura constante es muy eficiente ya que nos da un comportamiento general de la cinética del kerógeno. En dicho modelo se toman en cuenta la temperatura, energías de activación y factor de frecuencia. Sin embargo, a pesar de dar una muy buena aproximación, ésta no refleja la cinética exacta del kerógeno en condiciones reales; para tener una mejor aproximación sería necesario hacer una simulación del modelo a temperaturas variables, mediante el método de diferencias finitas; más aún, seguiría siendo una mera aproximación al verdadero comportamiento, puesto que las reacciones en un contexto real no son necesariamente sucesivas y paralelas, es decir, podrían ser totalmente irregulares.
Se observó que las energías de activación repercuten directamente en la transformación del kerógeno cuando tenemos una temperatura y factor de frecuencia constante. Esto debido a que al tener una energía de activación más alta se necesita una mayor temperatura para la degradación del kerógeno en sus diferentes productos.
Al hacer la simulación a temperatura constante para el caso del pozo IRME-1 notamos que una temperatura de 125°C no es suficiente para ver una transformación significativa del kerógeno x a sus respectivos subproductos y, u1 y u2.
El caso más favorable es el que tiene energías de activación bajas con temperaturas altas, el cual es el caso de la Simulación 3, en el que a una temperatura de 174°C tendríamos, según la simulación una predominancia de hidrocarburos, resinas y asfaltenos u1, en la actualidad en la zona de estudio.
Agradecimientos
Agradecemos al proyecto UACOAH-PTC-339 por el apoyo brindado para el desarrollo de este trabajo.
Referencias
Behar, F., Beaumont, V., Penteado, H. L. B., (2001), Rock-Eval 6 Tecnology: Performances and developments. Oil Gas Science and Tecnology-Rev. IFP, 56, 111-134.
Camacho, L. F., (2009), Origine-Evolution-Migration et Stockage, des hidrocarburos dans le bassin de Sabinas, NE Mexique: étude intégré de pétrograpgie, géochimie, géopgyque et modélisation numérique 1D-2D et 3D. Universidad de Nancy, 208 pp.
Corona, R., Trilla, J., Benavides, M. E., Sanchez, N. P. Ferrusquía, V., (2006), Geología, estructura y composición de los principales yacimientos de carbón mineral en México. Boletín de la Sociedad Geológica Mexicana, 141-160.
Goncalves, F. T. T., García, D. F., Penteado, H. L. B., Giraldo, B. N., Bedregal, R. P., Gómez, P., (2001), Cinética de la degradación del petróleo: Principios y aplicaciones en cuencas colombianas, 2, 27-41.
Mark, J. J., David, G. H., (1996), Thermal Maturity of Sedimentary Basins in Alaska, An Overview. U.S. Geological Survey Bulletin 2142.
Peters, E., Walters, C., Mankiewicz, P., (2006), Evoluciona of kinetic uncertainty in numerical models of petroleum generation, American Association of Petroleum Gaologists, 90, 387-403.
Johnson, J. M., Howell, G. D., (1996), Thermal Maturity of Sedimentary Basins in Alaska. U.S., Geological Survey Bulletin, 2142, 1-19.
Petróleos Mexicanos (PEMEX), (2013), Exploración y Producción, Provincia petrolera Sabinas-Burros-Picachos. Versión 2.0.
Resendiz, P. R., (2017), Historia de la generación de hidrocarburos de la Formación Eagle Ford en México: Implicación del análisis maceral, Universidad Autónoma de Coahuila. Escuela Superior de Ingeniería, 67 pp.
Tissot, P. B., (1969), Premières données sur les mécanismes et la cinétique de la formation du pétrole dans les sédiments. Simulation dun schéma réactionnel sur ordinateur, Revue de Institut Francais du Pétrole, 24, 470-501.
Tissot, P. B., Espitale, J., (1975), L`elolution thermique de la matière organique des sédiments: applications d`une simulation mathématique. Potentiel pétrolier des bassins sédimentaires de reconstitution de l`histoire thermique des sédiments, 30.
Tissot, P. B. Deroo, G., Hood, A., (1978), Geochemical study of the Uinta Basin: formation of petroleum from the Green River formation, 42, 1469-1485.
Tissot, P. B., Welte, D. H., (1984), Petroleum Formation and Ocurrence. Springer Verlag Berlin Heidelberg New York. Segunda edición revisada y alargada, 699 pp.
Tissot, P. B., (2003), Preliminary data on the mechanisms and kinetics of the formation of petroleum in sediments. Computer simulation of a reaction flowsheet, Oil & gas science and tecnology, 58, 183-202.
Servicio Geológico Mexicano (SGM), (2008), (a). Carta Geológica-Minera Nueva Rosita G14-A13, Coah., Esc. 1: 50,000. Segunda edición.
Servicio Geológico Mexicano (SGM), (2008), (b) Programa de Minerales Energéticos. Informe geológico-económico sobre carbón y gas asociado a yacimientos de carbón (GAC) del bloque San Patricio, municipios de Candela y Progreso, Coahuila y Lampazos, Nuevo León; México, pp. 70.
Servicio Geológico Mexicano (SGM), (2006), Léxico Estratigráfico de México. Formación olmos.


















