Caos y fractales en los depósitos minerales En busca de una aproximación abstracta de la realidad
Por: José Antonio Martínez Mendoza1
Introducción
Un explorador exitoso debe ser un profesional de las ciencias de la tierra con una sólida formación científica, aunque a diferencia del geo-científico puro tiene como único propósito el descubrir depósitos minerales de rendimiento económico. En la industria minera, esto supone una aparente dicotomía entre: “un ingeniero por formación y un geólogo por vocación”. Esta extraña amalgama entre una técnica por definición objetiva con una ciencia eminentemente subjetiva puede conducir en el mejor de los casos, cuando dicha amalgama es bien conceptuada, a lograr los propósitos del explorador que es el descubrimiento de nuevos cuerpos de mineral o bien encontrar nuevos yacimientos, asegurando la continuidad de operaciones en el primer caso o la apertura de nuevas en el segundo.
La comprensión adecuada del comportamiento de las estructuras mineralizadas es esencial en el proceso de exploración de un depósito mineral. Por esta razón, es muy común que quede recurrentemente registrado en la gran mayoría de los reportes técnicos que se publican, que el yacimiento en cuestión presenta invariablemente en su posición y forma un control estructural. Sin embargo, rara vez ocurre una explicación lo suficientemente coherente sobre dicho control. Esto es debido principalmente, a que el geólogo económico, rara vez también, cuenta con un conocimiento sólido sobre geología estructural, y no está fortalecido en las técnicas de predicción que se requieren. Si acaso, la mejor de las veces hay explicaciones que se ajustan mucho a las corrientes euclidianas como veremos más adelante.
“Un depósito mineral es un fenómeno de la naturaleza producto de un sistema caótico”. Esta aseveración, que se demostrará por sí misma en el desarrollo del presente artículo, es la base para lograr un mejor entendimiento sobre la formación de un depósito mineral y como consecuencia, si el geólogo carga con este entendimiento en su alforja, se le facilitará hacer predicciones sobre el comportamiento estructural de los cuerpos mineralizados con una aproximación abstracta mucho más cercana a la realidad que las que se hacen por medio de las técnicas convencionalmente empleadas.
El caos y la complejidad, que rigen la formación de un yacimiento, ocurren siempre en un tiempo y espacio despreciable, si los referimos por supuesto tanto a la escala del tiempo geológico como al espacio que ocupan en la corteza. Sin embargo, éste ínfimo momento en ese ínfimo espacio deja huellas de su paso que pueden ser aprovechadas. Con base en la geometría fractal – típica de un sistema caótico -, es posible, no sólo comprender bajo qué ambiente estructural fue formado un yacimiento, sino que permite una vez que han sido identificadas las evidencias fractales, registrar, procesar y analizar las mismas y ayudar al profesional a reducir el riesgo en sus predicciones, aumentando, por tanto, la probabilidad de éxito en la exploración.
Evolución de las predicciones en la naturaleza.
En el año de 1962, Thomas Kuhn postuló en su libro The Structure of Scientific Revolutions que la ciencia se desarrolla en dos etapas. Una a la que denomina ciencia normal, y otra a la que llama ciencia revolucionaria. La primera está caracterizada por la acumulación de conocimientos, sin cuestionamientos, de los paradigmas aceptados por la comunidad científica y la segunda aparece cuando se rompen los cauces de ese conocimiento y se establecen nuevas concepciones teóricas.2 Basado en el postulado de Kuhn, es posible sugerir que la evolución de las predicciones en las ciencias de la naturaleza, ha tenido por lo menos tres grandes épocas revolucionarias.
Primera Revolución: Copernicana
Eran los albores del s. XVI, y habían transcurrido más de quince siglos del mundo moderno, y la única ciencia disponible era la astrología, es decir, el estudio de la posición y movimiento de los astros como medio para predecir hechos futuros y carácter de las personas3. Esta ciencia hasta entonces normal, fue acaparada y utilizada por gobernantes, monarcas y jerarcas religiosos. Renombrados astrólogos, dirigían, en el peor de los casos tras bambalinas, el mundo con sus predicciones. Origen sin duda de la astronomía apoyándose en la primera parte de su definición, tuvo por otro lado, una dosis importante de superchería, charlatanería, fraudes e intereses ocultos que se asomaban cada vez con más sofisticación conforme se iba obteniendo poder, distorsionando y corrompiendo el saber científico.
El orden de la astrología como ciencia normal, se rompe al aparecer publicado en 1507 Sobre las revoluciones de los orbes celestes del astrónomo polaco Nicolás Copérnico4, donde se formula la teoría heliocéntrica o como los astros del Sistema Solar giran alrededor del sol. Esta revolucionaria idea, acompañaría al Renacimiento europeo y generaría un profundo cambio en las convicciones filosóficas, marcando un hito en las ideas y cultura predominantes en la época. Casi un siglo después, en 1609, Galileo-Galilei confirmaría con sus observaciones telescópicas sobre los astros mediceos – las lunas de júpiter – la teoría de Copérnico y formularía las primeras leyes sobre el movimiento de los astros. Lo seguiría, el astrónomo alemán Kepler que en 1619 publicaría la última de sus leyes en su estudio Sobre la armonía del mundo, donde numéricamente relaciona los planetas en relación a su distancia al sol.5
Segunda Revolución: Determinista
Dos siglos casi transcurrieron desde que Copérnico revolucionara la ciencia y hubiera basado en ella una nueva corriente normal en las investigaciones científicas, que serían continuadas por Galileo y Kepler, y se da la culminación de esta corriente científica cuando aparece en escena en 1687, Isaac Newton revolucionando por segunda vez la ciencia al publicar sus Principios Matemáticos de la Filosofía Natural, donde se hallan expuestas las célebres “Leyes de Newton”. Conocedor de las leyes de Kepler sobre las órbitas de los planetas y de los estudios de Galileo, estableció en sus Principios Matemáticos de la Filosofía Natural, las leyes fundamentales de la dinámica y dedujo de ellas su famosa Ley de Gravitación Universal. La clarificación y formulación matemática deslumbró a la comunidad científica de la época. Creó la física clásica y lo que se conoce como determinismo científico que se mantendría vigente por lo menos durante los siguientes dos siglos, hasta las postrimerías del siglo XIX. Uno de los máximos exponentes del determinismo científico que imperó como ciencia normal durante dos siglos, fue el matemático francés Pierre Simon de Laplace que en 1776 afirmaba categóricamente: “… si se conociera la velocidad y posición de todas las partículas del universo en un instante dado, entonces se podría predecir su pasado y futuro para el resto de los siglos” 6.
Tercera Revolución: Caos y Complejidad
A diferencia de los cambios drásticos detonados por los revolucionarios Copérnico y Newton en las Revoluciones Copernicana y Determinista respectivamente, que se dieron a partir de sendas publicaciones científicas; la tercera revolución tiene una historia más azarosa, pues por lo menos tres etapas de rompimiento de paradigmas científicos han ocurrido, desde finales s. XIX. (1892) hasta las postrimerías del s. XX. (1982). La comunidad científica sabía, sin poder demostrarlo, desde finales del s. XIX, que la implícita rigidez determinista impedía explicar muchas de las perturbaciones que ocurrían en la naturaleza. Se asumía, en todo caso que los fenómenos fortuitos o azarosos son, por definición, aquellos cuyas leyes ignoramos.
El primer rompimiento del paradigma determinista se da en 1892. El físico y matemático francés Henry Poincaré, ingeniero de minas (llegó a ejercerla profesionalmente) fue el primero – al menos del que se tiene registro – en plantear formalmente las perturbaciones en términos científicos en el concurso de ciencia que había promovido el rey Carlos II de Suecia para celebrar su cumpleaños sesenta. Tras tres años de ardua investigación, presenta resultados en su ponencia Métodos Nuevos de la Mecánica Celeste, donde confirma la inestabilidad del Sistema Solar, concluyendo que el movimiento de los cuerpos del Sistema Solar prácticamente no se repetía nunca, al menos con total exactitud. Paradójicamente, el futuro, a pesar de ser determinista, era impredecible.7
El segundo rompimiento y que es representativo de esta revolución de la ciencia está a cargo de Albert Einstein con su famosa Teoría de la Relatividad, sin duda uno de los logros más importantes de la física moderna. Fue Publicada en 1916. Einstein propuso que en presencia de materia y energía, el espacio se puede deformar, formando crestas y valles que causan que los cuerpos se muevan por estas rutas irregulares. Así que, aunque la Tierra se mueve alrededor del Sol, en realidad, la irregularidad persiste y es simplemente la geometría del espacio-tiempo alrededor del Sol la que le dice cómo debe moverse. La teoría de la relatividad general, no sólo explica el movimiento de los planetas, sino que también puede describir la historia y la expansión del Universo, la física de los agujeros negros, la curvatura de la luz de las estrellas y las galaxias distantes.8
En 1975 se generó el tercer rompimiento de paradigmas. La comunidad científica, se había desbordado por la investigación hacia los fenómenos irregulares y complejos. Es así como se comienza a hablar incesantemente de caos, complejidad, turbulencia, irregularidad, desorden, para explicar muchos de los fenómenos de la naturaleza que se caracterizan por tener un comportamiento que no puede ser descrito por leyes matemáticas sencillas. Mas extraño aún resultaba el hecho de que este tipo de caos emergía de fenómenos cuya evolución es inicialmente determinista 9.
El máximo exponente de este rompimiento es Benoit Mandelbrot. En sus investigaciones acerca del tema, que le llevan más de 30 años (1951-1982), Mandelbrot terminó por acuñar el término fractal para describir formas geométricas cuya estructura se repite en cada una de sus partes, y en las partes de sus partes. Su obra La geometría fractal de la naturaleza (1982), marca un hito en la concepción de la ciencia. Hoy en día la geometría fractal, una aproximación más abstracta de la realidad a la dimensión que caracteriza a la geometría convencional, aparece como una explicación lógica a las perturbaciones caóticas. Así, queda implícita en la distribución de galaxias, en las irregularidades de una costa, en las de una montaña, en la forma de un río, en las variaciones del clima e incluso en el latir de un corazón. Se ramifican en nuestro cuerpo en alvéolos y redes neuronales como evolución de sistemas caóticos, constituyen la huella de fallas y fracturas en la corteza, epicentros de temblores, aparecen en la repetición de palabras de un texto, en la variación del clima e incluso en las fluctuaciones de precios de mercado.10
Acerca de las predicciones a partir de las revoluciones científicas
Aun cuando en la actualidad la comunidad científica ha venido adoptando el caos y fractales para explicar las perturbaciones de los sistemas aparentemente desordenados y hacer predicciones sobre su comportamiento; todavía no es común que estos se utilicen en la geología económica. Lo que, si resulta muy común, es que los profesionales de las ciencias de la tierra continúen – en el mejor de los casos -, utilizando el determinismo científico en sus predicciones. Este determinismo es válido para ciertos casos sin duda, la astronomía, por ejemplo, sigue utilizándolo con éxito en sus predicciones sobre la mecánica celeste; pero al momento de hacerlas sobre el comportamiento estructural de los sistemas mineralizados que por definición son caóticos no resulta – a la luz de la ciencia actual – un procedimiento efectivo.
Lo anterior no es de extrañar, pues el caos y los fractales están en proceso de volverse paradigmas científicos debido a su reciente incorporación a la filosofía de la ciencia. Históricamente, las revoluciones científicas han tardado un siglo o más en consolidarse y todavía después de transcurrido este tiempo de consolidación aparecen detractores o impulsores de otras corrientes. La astrología es el mejor ejemplo de esto. A pesar que la revolución Copernicana (1507) dio un giro completo a la concepción de la ciencia en el mundo, siguieron apareciendo, incluso siglos después, exitosamente astrólogos en el escenario como Nostradamus (1553), Ruggeri (1600), Rasputín (1900). Otros no sólo se quedaron en la aplicación de los antiguos paradigmas, sino que también resultaron ser grandes detractores a los nuevos paradigmas que se sucedían, es el caso de Martin Horky (1615) quién atacó con saña a Galileo defendiendo a la astrología más de un siglo después de Copérnico; es famosa su frase: “Los astrólogos han hecho sus horóscopos teniendo en cuenta todo aquello que se mueve en los cielos. Por lo tanto, los astros mediceos no sirven para nada y como Dios no crea cosas inútiles estos astros no pueden existir”. Además de detractores, también la historia de la ciencia ha sido testigo de grandes disputas científicas. Durante la tercera revolución y en plena efervescencia del orden y el caos, en 1944, el físico danés Niels Bohr, responde a la famosa frase de Einstein: “Dios no juega a los dados con el Universo”, replicándole: “¡Einstein, deje de decirle a Dios lo que tiene que hacer!”11.
Las técnicas de predicción sobre el emplazamiento, ubicación y forma de los yacimientos minerales utilizadas en la actualidad para el descubrimiento de nuevos cuerpos minerales o yacimientos se basan en el mejor de los casos en análisis sofisticados de información determinista: geoquímica multivariable, firmas geofísicas, espectrales, alteraciones, geoquímica de inclusiones, termometría y comportamientos estructurales euclidianos entre otros. En todos los casos la cantidad de información es esencial: “a mayor cantidad de datos la probabilidad de error disminuye”. Esto último resulta no esencial ni válido en sistemas caóticos como veremos. Lamentablemente, todavía en pleno s. XXI, se dan casos de predicción emulando a astrólogos aficionados, o bien basados en la radiestesia12, varas, sensaciones paranormales o simples intuiciones. (Figura 1)
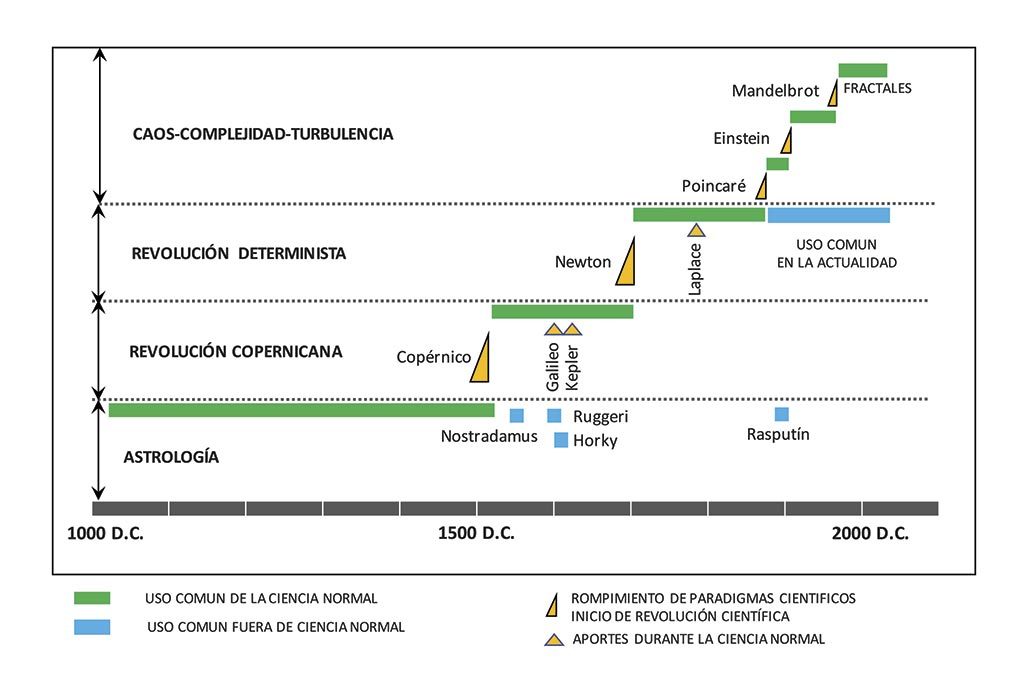
Lejos de ser preocupante, se infiere que estas tendencias predictivas dejarán de estar en boga de manera paulatina y que aún los métodos deterministas por muy sofisticados que parezcan también dejarán de estarlo y el caos y los fractales irán ganando terreno conforme se profundice en las investigaciones en este campo y las predicciones que se hagan con dicha base se acerquen más a la realidad.
Caos en los depósitos minerales
El caos se da cuando un sistema determinista, que está regido por leyes bien precisas, tiene un comportamiento estocástico-determinista, esto es que el sistema al pasar de un estado a otro sólo puede ser descrito en términos de probabilidad. En un sistema no caótico (ordenado o determinista), el conocimiento del pasado es suficiente para predecir el futuro, en uno caótico, no importa cuantos datos tengamos del pasado, no podemos predecir el futuro, sólo definir probabilidades13.


Una situación importante que sucede en la naturaleza frecuentemente es que un sistema ordenado puede volverse caótico y un sistema caótico puede volverse ordenado. A pesar de esto, prevalece el orden y entonces puede hablarse de Caos Determinista. Un buen ejemplo de Caos Determinista lo propone Yacamán14 al explicar lo que sucede en el flujo de un río (Figura 2): Primero el río tiene en su lecho rocas y el flujo de agua está tranquilo, mientras esto continúe así, es decir ordenado, las predicciones que hagamos sobre el flujo, movimiento, turbulencias, incluso partículas en suspensión serán deterministas como puede inferirse de la figura 2 (A y B). De repente, en cuanto comienza a aumentar el caudal del río, se va desordenando alrededor de las rocas y finalmente se produce una turbulencia muy fuerte alrededor de ellas. El resultado es una nueva distribución de rocas, esto corresponde a un sistema caótico (Figura 2, B y C). En este caso no pueden predecirse distribuciones a partir de datos deterministas previos, sólo definirse probabilidades. El sistema por fin vuelve al orden. Es indudable que el paso del caos en el río dejó huellas, un nuevo paisaje. Paradójicamente, estas huellas presentan un orden nuevo, es decir hay orden en el caos. Contrariamente a lo que podría esperarse, al aumentar la cantidad de información disponible del sistema ordenado no se evita la imposibilidad de conocer la progresión futura del sistema.
Aún en la literatura, el concepto de caos es protagonista como en El pintor de batallas15 de Arturo Pérez-Reverte (2006): “Hace ya medio siglo que sabemos que las verdaderas leyes no pueden ser lineales. En aquellos sistemas confortables con los que la ciencia nos tranquilizó durante siglos, los cambios minúsculos no alteraban la solución; pero en los sistemas caóticos, cuando varían un poco las condiciones de partida, el objeto sigue un camino distinto […] pero es verdad que un sistema caótico está sujeto a leyes o reglas. Es más, hay reglas hechas de excepciones, o de azares aparentes. Resumiendo, amigo mío, aunque no lo parezca, hay orden en el caos”.
Al explicar la forma y distribución aleatoria de las estructuras de la corteza terrestre, Chelén-Franulic postula: “el desorden en la naturaleza no existe”16.
Se asoma vigorosamente el concepto de aleatoriedad, azar y caos. Tal vez sólo había que reafirmarlo completando el postulado: “… cuando no hay orden hay caos”.
Muchos de los fenómenos aleatorios o caóticos son metafóricamente como el polvo de la casa que a veces se suele esconder cómodamente debajo de la alfombra17. Sin embargo, a pesar que se niegue, su existencia es contundente. Es obvio que el polvo afea el orden y lo convierte en desorden. Al ignorar el desorden, asumimos entonces como algo que nunca debió haber existido y en las ciencias usualmente se le acusa de delincuente que viola “las leyes de la naturaleza”. Mandelbrot al referirse a los datos crudos que marcan ruptura en su distribución sin explicación aparente. Sugiere que, en lugar de eliminarlos, deben ser tratados con especial interés. Concluye: “no se deben ocultar los datos incómodos bajo la alfombra”.18
Los yacimientos minerales son anómalos en su composición, caprichosos en su ocurrencia y enigmáticos en su origen, de ahí la complejidad que encierra su descubrimiento. La ocurrencia obedece a que una región de la corteza terrestre debe tener propiedades sine qua non: preparación estructural, historia térmica, ambiente supracrustal, erosión, tiempo necesario para la mineralización y rocas susceptibles de reaccionar con los fluidos mineralizantes y/o albergarlos 19.
En el año 2002, Singer et al 20 llevan a cabo un estudio sobre la distribución en el mundo de los depósitos tipo pórfido y asociados, que engloba la mayor cantidad de depósitos metálicos conocidos. Su análisis confirma, sin sorpresas, que los depósitos metálicos en el mundo espacialmente se encuentran estrechamente ligados a la fuente magmática que los origina. Sugiere por su análisis que el radio de influencia máxima a partir del foco de calor es de 10 kilómetros, área donde pueden encontrarse cuerpos de skarns polimetálicos (Cu-Zn-Pb), vetas polimetálicas, yacimientos epitermales de Au-Ag, brechas freatomagmáticas e incluso placeres y depósitos exóticos. Por otro lado, es bien sabido que la vida de un sistema geotérmico o magmático ocurre en un rango de 5 a 20 millones de años inclusive para los muy longevos, tiempo durante el cual evoluciona de tal manera que en un instante de su vida se produce la mineralización. Camprubi et al 21 en su análisis de los depósitos epitermales de baja y alta sulfuración, reporta que la diferencia de edad entre las rocas ígneas genéticamente asociadas a la mineralización, como generadoras de esta o como foco de calor, muestran un corto rango, por lo general entre 0.3 y 4 m.a.
Simplificando. Existen dos condiciones esenciales para que un yacimiento mineral sea formado: fluidos mineralizantes y una trampa estructural para que estos se depositen y por supuesto es indispensable que estas condiciones coincidan en el espacio y tiempo, que como hemos visto resultan despreciables en escala, tanto en su dimensión geográfica como en el tiempo geológico. Entonces, resulta lógico suponer que las perturbaciones al orden establecido en el espacio y tiempo donde ocurre la mineralización son el polvo bajo la alfombra del sistema geotermal y a su vez el sistema geotermal es el polvo bajo la alfombra de la evolución tectónica de una región determinada. Así pues, dichas perturbaciones del orden establecido estarán regidas por un sistema caótico.

(a) Interpretación euclidiana incorrecta ( por lo regular muy común) sobre el patrón observado.
(b) Note que aparece un patrón de fallas inexistentes con movimiento lateral dextral interpretado.
Un sinnúmero de ejemplos de mineralización, evidencia que la anterior proposición lógica es correcta. En la Figura 3, se muestran algunos ejemplos de cómo la mineralización en vetas ocurre en un tiempo sumamente restringido en la vida de las mismas. Se puede proponer en términos generales que, en la formación de una veta, el clímax de la mineralización ocurre apenas en un diez por ciento del tiempo de su formación y ocupa un espacio en la misma proporción.
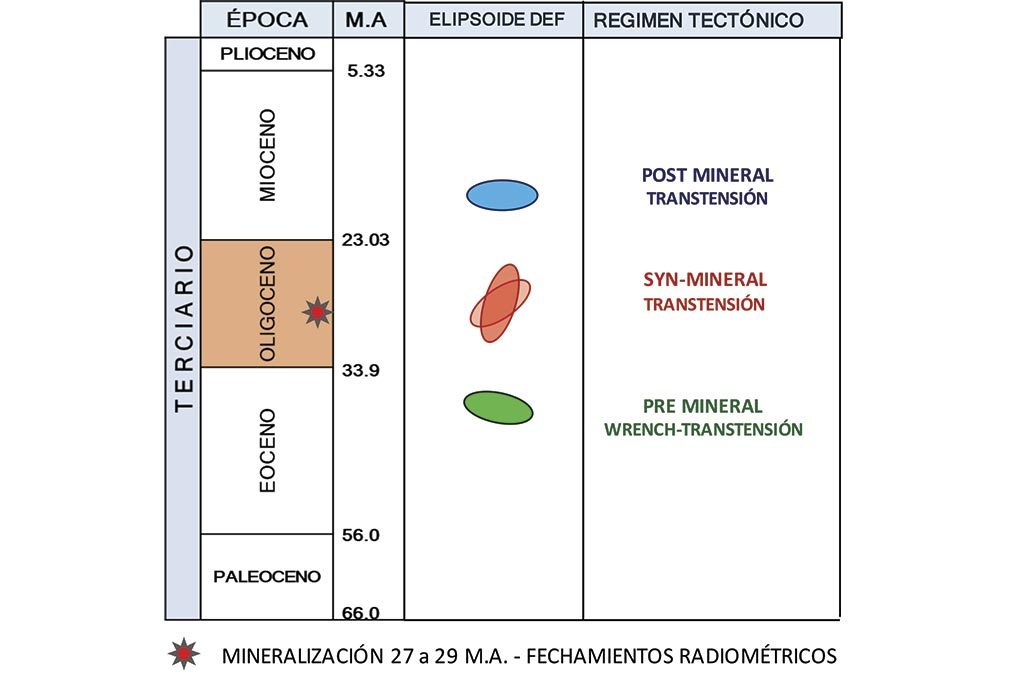
Un ejemplo bien documentado, basado en mediciones en campo de como ocurre una mineralización regida por el caos es el distrito minero de Guanajuato 22, lo propone el autor en 1995: (Figura 4) “durante el Cenozoico y antes de la mineralización que se produce en el Oligoceno (27-29 m.a.), tectónicamente la región fue objeto de varios pulsos tectónicos que produjeron a su vez fallamiento, sin embargo el sistema desde este punto de vista se considera fue ordenado ya que la dirección de la extensión fue la misma durante estos pulsos (W-NW/E-SE); por alguna razón, que se infiere fue el domamiento del manto, la extensión rota en determinado momento y durante un período corto de tiempo hacia una dirección N-NE/S-SW. El domamiento junto con la formación de fallas y reactivación de otras viene acompañado de magmatismo que aprovechó las zonas de dilatación formadas para su ascenso inclusive a superficie. El gradiente geotérmico inducido por este magmatismo provoca además que el sistema actúe y rellene con mineralización las zonas de dilatación provocadas con este nuevo régimen tectónico. El conjunto de estos fenómenos que ocurren en un lapso de tiempo geológico muy corto es el que se considera un sistema caótico. Una vez que cesa el caos el sistema vuelva a ordenarse rotando una vez más la dirección de la extensión regional hasta ubicarse en W/NW/E-SE, posición que presentaba antes del caos y que guarda hasta el presente inclusive”.
Fractales en los Depósitos Minerales
El hombre se ha obsesionado por entender a nuestro mundo en perfecta armonía resultado de reglas simples y ordenadas, y generalmente el desorden, cuando se detecta, es considerado producto del azar. Por esta razón, cuándo tres siglos antes de la era cristiana, el matemático griego Euclides en su afamada obra Elementos propuso de manera formal los teoremas sobre las propiedades de líneas y planos, círculos y esferas, triángulos y conos, etc.; es decir de las formas regulares, estos dieron la explicación científica idónea con que se tranquilizó al mundo nada menos que durante 23 siglos. Si bien es cierto que los postulados de Euclides, además de ser poderosos instrumentos de razonamiento deductivo han sido extremadamente útiles en muchos campos del conocimiento, la física, matemáticas, diversas ingenierías, la astronomía, etc.23 También sabemos que las ideas de Euclides constituyen una considerable abstracción de la realidad, sobre todo en sistemas no lineales o no ordenados en la naturaleza.
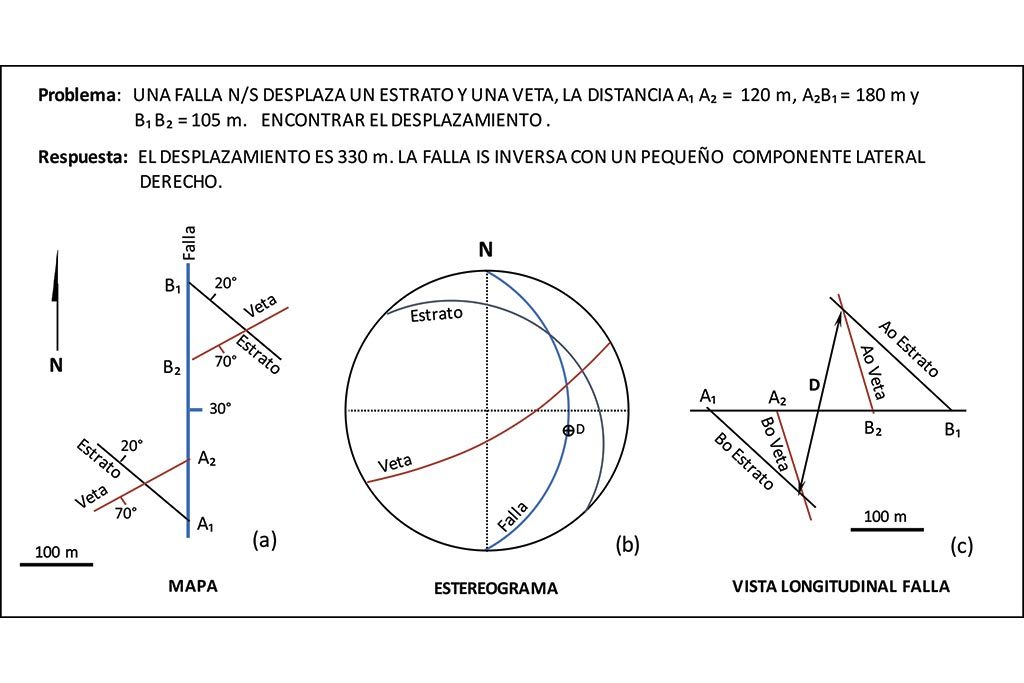
A pesar de esto, las ciencias de la tierra, específicamente la geología estructural, se ha apoyado históricamente en conceptos euclidianos, no solo para explicar (Figura 5), sino para analizar comportamientos, resolver problemas estructurales y hacer predicciones sobre los mismos (Figura6).
El uso común para resolver problemas sobre bases euclidianas y deterministas en la geología estructural se ha convertido en un hábito. Se aplican métodos matemáticos como teoría de vectores, geometría analítica, proyecciones estereográficas y otros en la resolución de problemas y hacer predicciones y estos métodos han venido siendo depurados cada vez y con más sofisticación para su uso en forma de softwares especializados. Sin duda, la base euclidiana y determinista apoya en la comprensión y ayuda en la predicción, pero es innegable que dichas predicciones son una abstracción muy alejada de la realidad pues los fenómenos tectónicos que generan esas perturbaciones en la corteza en forma de fracturas, pliegues y fallas obedecen más a un régimen caótico (Figura 7a), que no puede explicarse con la certeza requerida por métodos convencionales e incluso dan lugar a una distorsión de la realidad, alejándose de ella, muchas de las veces en una opuesta dirección. No es raro encontrar explicaciones euclidianas incorrectas a problemas caóticos como puede observarse en el ejemplo de la Figura 7b.
Analizar y estudiar las perturbaciones de los sistemas ordenados resulta tan relevante para entender los fenómenos de la naturaleza que esto no puede ser despreciado, a pesar, y precisamente, porque dichas perturbaciones desarrollan patrones asimétricos. Estos patrones asimétricos se manifiestan como un conjunto de formas que poseen detalle a toda escala, no son diferenciables y exhiben dimensión fraccional 24.
Según Talanquer 25, el interés de Mandelbrot en el tema nació de su certeza de que “las nubes no son esferas, las montañas no son conos, las costas no son líneas ni círculos, como la corteza de un árbol no es plana ni un rayo viaja en línea recta”, y que por otro lado, confirmaba que: “una roca es similar a la montaña de la que forma parte; una rama tiene la misma estructura que la del tronco del que nace; como si la decisión hubiera sido repetir la misma forma a diferentes escalas dentro de un mismo objeto, asegurando una copia del original a cualquier nivel de amplificación, como si se pensara en generar el máximo nivel de diseño con el mínimo costo. Un helecho, un brócoli o una coliflor son muestras vivas de este juego de la naturaleza en el que el mismo patrón de crecimiento se manifiesta a diferentes escalas”. Estos conceptos le llevaron a definir las reglas de la geometría fractal, adoptando nuevos paradigmas a la ciencia como hemos visto.
Recapitulando, vayamos a la explicación que el mismo Benoit Mandelbrot 26 (padre de la geometría fractal) da sobre el origen de su interés en el tema. La idea detonó en 1951 al final de una visita a su tío (hombre de ciencia), cuando éste le comentó al despedirse: “toma esta separata. Es el tipo de tontería que sólo te puede gustar a ti”. El texto era una reseña de la revista Scientific American de un libro titulado Comportamiento humano y el principio del mínimo esfuerzo, escrito por George K. Zipf. El tema era por demás extraño: una fórmula matemática de una sencillez absurda sobre el patrón de frecuencia de palabras de comunes a raras en un texto que se cumplía no importaba el idioma utilizado ni el grado de formación del escritor. Un análisis cuidadoso de los gráficos mostraba ruido o irregularidades notables. En poco tiempo aparece la fórmula Zipf-Mandelbrot.
Más tarde Mandelbrot abandona a Zipf y guiado por una necesidad lógica, el azar puro, lo conduce a continuar investigando contra todos los paradigmas hasta entonces aceptados por la comunidad científica. Así, en 1967 aparece su artículo ¿Cuánto mide la costa de Gran Bretaña? donde expone sus ideas tempranas sobre el tema al concluir: “la dimensión es infinita y todo depende de la regla con que se mida y del tamaño de mapa que se utilice”. Los estudios que Mandelbrot sigue llevando a cabo sobre el caos y la complejidad le llevarían en 1975 a acuñar por fin la palabra “fractal” para explicar aquellas formas geométricas complejas caracterizadas por la auto semejanza y capaces de describir aquellos fenómenos espaciales no uniformes para los que las formas geométricas euclidianas habituales resultan insuficientes y que rigen a la naturaleza. Tiempo después, en 1982 publica la máxima de sus obras: La geometría fractal de la naturaleza con el que logró un mejor conocimiento sobre la complejidad, turbulencia o irregularidad en la naturaleza. La geometría fractal desde entonces ha venido siendo utilizada para explicar aquello que la geometría convencional euclidiana no hace con suficiencia.
Queda, entonces, acuñada la definición de fractal (del latín fractus, irregular, fragmentado) como la configuración geométrica que posee la notable propiedad de presentar siempre el mismo aspecto por muy cerca que se le examine. Para explicarlo, Mandelbrot 27 menciona que al estudiar la turbulencia o caos en un sistema se dio cuenta que la posición de un punto en un instante de tiempo define su posición en el instante siguiente siguiendo aproximadamente una dinámica cuadrática. Al iterar, es decir repetir sin fin, la iteración define una figura abrumadoramente rica en detalles y minuciosamente sutil. Contrariamente a lo que sucede cuando se hace esto para una figura regular euclidiana.
“Inagotables maravillas nacen de reglas simples […] repetidas sin fin” diría en su última conferencia en Long Beach, California en 2010 al explicar el conjunto de Mandelbrot 28 (Figura 8). Revivía así la frase de Carlos Darwin: “innumerables formas bellísimas y prodigiosas han evolucionado a partir de un origen tan simple y continúan haciéndolo”. Desde entonces, el término fractal se ha extendido a pasos agigantados a tantas mentes, libros e investigaciones que cuesta creer en la actualidad que haya sido acuñada apenas en 1975.
Cuando un sistema muestra que cada una de sus partes es igual independientemente de la escala en la que se observe y estas poseen, desde el punto de vista matemático, propiedades peculiares que las distinguen, se revela la propiedad típica más importante de la geometría fractal: la autosimilaridad, donde un fractal es aquella fracción de un sistema caótico que tiene la característica de ser recursiva, es decir, un patrón externo se repite a si mismo a

diferentes niveles interiores, y así, sucesivamente hasta el infinito, de manera análoga a niveles externos: de lo infinitamente pequeño a lo infinitamente grande y viceversa. La autosimilaridad está presente siempre en los rasgos estructurales de la corteza terrestre dado que las deformaciones a las que está sometida ésta y que forman pliegues, fracturas, fallas y cualquier otro rasgo estructural, son producidas por fenómenos caóticos.
La autosimilaridad, entonces, como característica de la geometría fractal se convierte en indispensable si se desea acercarse a la realidad y con más exactitud y precisión que la geometría euclidiana, pues a través de ella es posible inferir la existencia de estructuras mayores a partir de estructuras en pequeña escala y viceversa porque la misma regular irregularidad persiste.
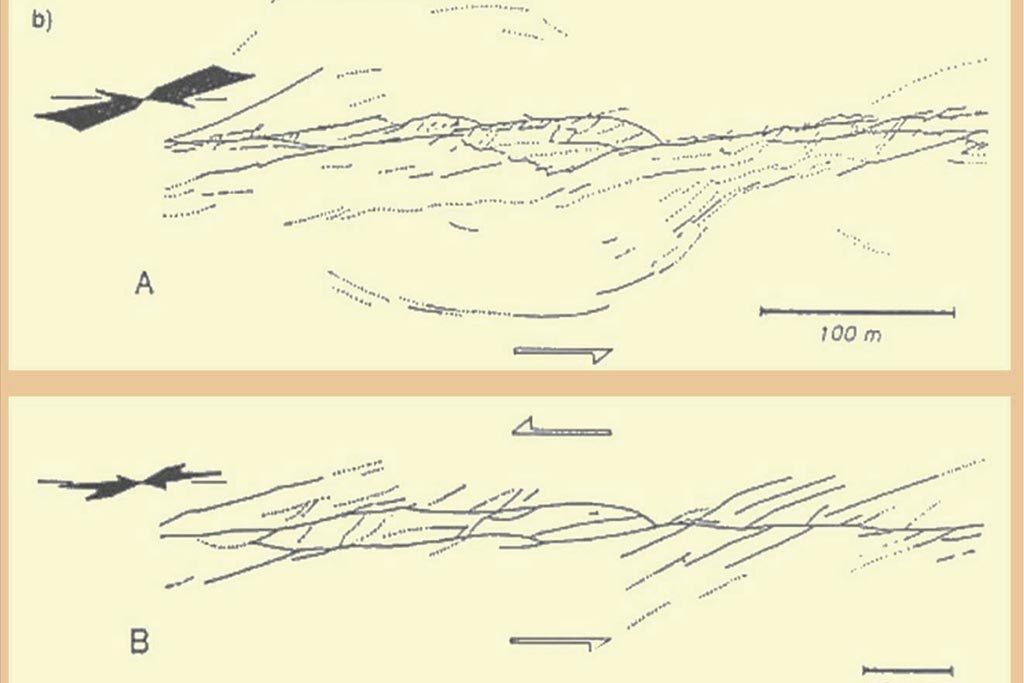
(tomado de Hoobs, 1976).
En la Figura 9, se muestra el patrón de fallamiento a lo largo de la falla Dash-e Bayaz, en Irán, formada por el terremoto de 1968, (Hoobs et al, 1976). Ilustra el comportamiento autosimilar de la misma a diferentes escalas. Puede notarse que un fractal (B), obtenido de la misma, muestra características que si bien no son iguales en forma estricta si son autosimilares al comportamiento a mayor escala.

Análisis estructural con base en geometría fractal
Una vez confirmado que un depósito mineral es un fenómeno de la naturaleza producto de un sistema caótico y que su ocurrencia obedece a que el sistema ordenado al que pertenece sufrió perturbaciones (caos) en un instante dado y en un breve espacio de una región determinada, permitiendo a los fluidos mineralizantes disponibles evolucionar, reaccionar y emplazarse en trampas estructurales que fueron generadas o reactivadas mientras estuvo en caos. Es entonces lógico suponer, que dado que el sistema no es ordenado mientras ocurrió la mineralización, las estructuras perturbadas durante este lapso y formadoras de trampas, estén regidas por la geometría fractal y muestren por tal motivo las principales características de este tipo de geometría como la recursividad y la autosimilaridad.
El reconocer la mineralización es uno de los elementos clave para llevar a cabo un análisis estructural. Este punto es esencial para concluir que el caos y fractales no están aislados de la geología ni mucho menos, al contrario, un conocimiento sólido de ésta es esencial para hacer las predicciones con una aproximación más exacta y precisa. Si en una región, distrito o cuerpo mineral es posible identificar la etapa mineralizante, entonces es posible registrar, procesar y analizar adecuadamente las evidencias fractales y lograr determinar si la estructura que aloja los cuerpos tuvo movimiento o no y si lo tuvo de que tipo fue, en qué ambiente tectónico se formó, como están definidas las zonas dilatadas o trampas estructurales e incluso que tipo de comportamiento se predice a mayor escala y por supuesto, definir los principales controles de la mineralización. Todo el cúmulo de información que arroja la comprensión de la geometría fractal de los cuerpos, dará como resultado hacer predicciones más confiables y reducir por consecuencia y considerablemente, el riesgo que esta actividad tiene implícita.
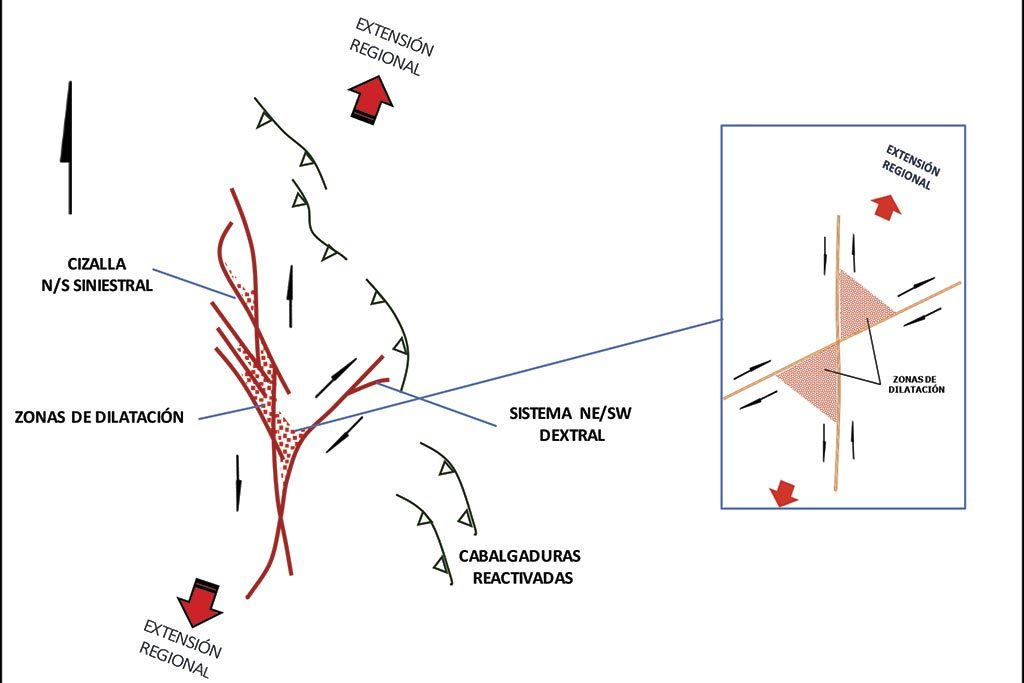
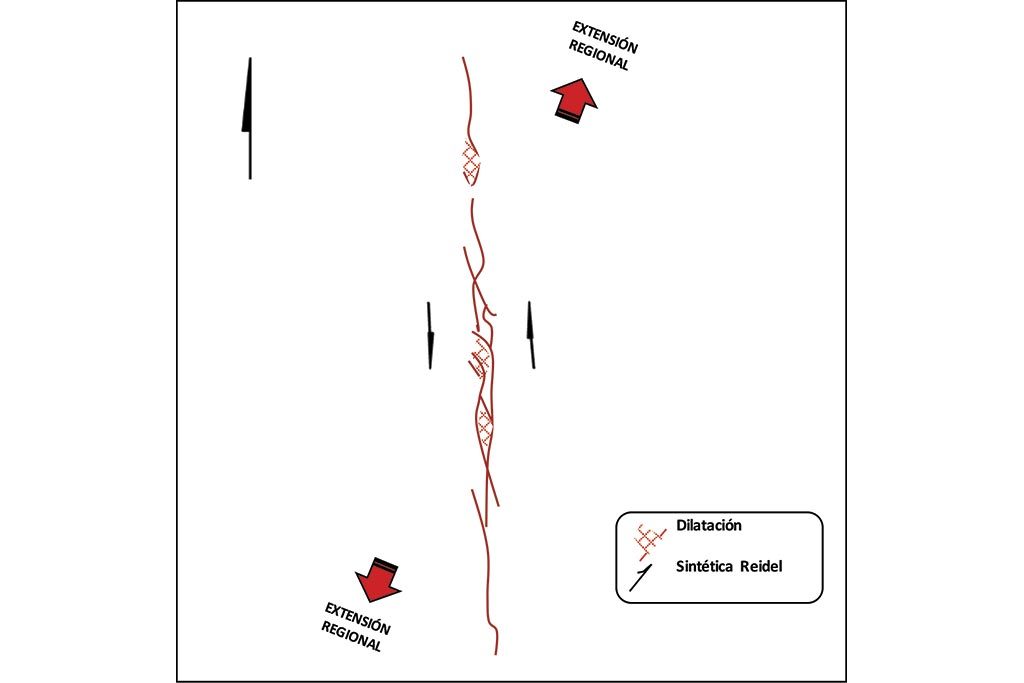
En una región frágil – muy común en las zonas que el geólogo económico explora – un fractal de una veta epitermal productiva en dirección N/S, obtenido en el piso de una galería subterránea, registra el momento de la mineralización y el menor esfuerzo (σ3 local medido en campo (NE/SE 45°)) en el que esta zona dilatada fue formada. Aquí, ya es posible determinar que la veta estudiada puede ser clasificada como una falla planar oblicua de alto ángulo con movimientos normales y laterales relativos izquierdos (siniestrales) alojada en un corredor estructural de deformación no co-axial y que desarrolla varios juegos de estructuras intra-cizalla, (Figura 10).
Un análisis de esfuerzos da como resultado la estimación del vector de máximo desplazamiento o Extensión Regional (σ3) al tiempo de la mineralización en una dirección NE/SW 22° y con esto puede proponerse el Sistema Regional de Esfuerzos (SRE) bajo el cual se formó la zona dilatada que contiene mineralización en la estructura. La disposición del SRE al tiempo de la mineralización en relación al corredor estructural indica que dicho corredor con dirección preferencial N/S, desarrolla un cizallamiento simple (Simple Shear) con movimientos laterales relativos izquierdos (siniestral) que junto con el movimiento normal observado produce un fallamiento oblicuo normal formado bajo un régimen tectónico típico de transtensión en zonas de estiramiento cortical.
No puede ser rebatido que, dado que el sistema estructural mineralizado ocurre en un instante de tiempo, aparecerán una gama de estructuras que se formaron previamente a la mineralización, otras durante la misma e incluso algunas posteriormente. Análisis de la geometría fractal de todas estas es esencial para definir los principales controles estructurales que presentará la mineralización. En el caso que nos ocupa, además de la principal orientación de la cizalla N/S a N-NW/S-SE, pudo determinarse que al tiempo de la mineralización se formaron estructuras pinadas internas W-NW/E-SE clasificadas como secundarias al corredor principal de la cizalla, su presencia marca la posición de zonas de dilatación. Un sistema NE/SW también está presente en el área y aparentemente fue reactivado al tiempo de la mineralización. Estructuras inversas de bajo ángulo NW/SE (cabalgaduras) que muestran una clara vergencia al NE también fueron observadas y analizadas y se interpretan como estructuras antiguas reactivadas al tiempo de la mineralización. Un análisis cuidadoso, que involucra las estructuras reconocidas y analizadas en sus diferentes etapas permite proponer los modelos conceptuales sobre los controles estructurales de la mineralización (Figura 11). Por último, con base en la geometría fractal del punto inspeccionado, en el grado de transtensión estimado y en modelos experimentales en zonas frágiles sometidas a este tipo de esfuerzos se puede predecir el comportamiento general que tendrá la estructura estudiada. (Figura 12).
Resulta cierto, aunque pueda resultar sorprendente, que un solo dato de la geometría fractal puede llevarnos a entender el comportamiento de una veta, definir controles y predecir comportamiento o nuevas trampas. Para reafirmar esta aseveración, hay que recordar que una de las premisas al hacer predicciones con bases euclidianas-deterministas es que la cantidad de información es importante: “a mayor cantidad de datos hay más confiabilidad”, y aunque hay algo de verdad en esto, pues a mayor cantidad de datos las predicciones tenderán a lograr la precisión, aunque no necesariamente la exactitud. Pero, dado que un depósito mineral es formado por un sistema caótico y en el caos no importa cuantos datos tengamos del pasado y que una buena comprensión de su geometría fractal puede llevarnos con poca información valida a obtener además de precisión, exactitud, logrando con esto hacer las predicciones con una abstracción mucho más cercana a la realidad que la que se hace con los métodos euclidianos y deterministas.
Registrar, procesar y analizar los datos aun cuando estos resulten pocos en cantidad revive la esencia del geólogo económico incitándolo más a la observación, análisis y comprensión con base en el conocimiento que a la metodología determinista de procesamiento de datos y uso indiscriminado de información que desafortunadamente continúa en auge. Por último, cabe destacar una frase atribuida a José Emilio Pacheco (J.M. Berlanga, comunicación personal): “Cuando la información sustituye al conocimiento, estas enterado de todo, pero no sabes nada de nada”.
Referencias
- Arenas, J, Departamento Física, Instituto Monterroso, Málaga España. 2014, ¿Es estable el Sistema Solar?, Revista Lat. Am. J. Phys. Educ. Vol. 8, No. 2, June.
- Braun, E., 1999, Caos, fractales y cosas raras, Segunda Edición La Ciencia para todos, Fondo de Cultura Económica.
- Camprubi, A., González-Partida, E., Levresse, G., Tritlla, J., Carrillo-Chávez, A., 2003, Depósitos epitermales de alta y baja sulfuración: una tabla comparativa, Boletín de la Sociedad Geológica Mexicana, Tomo LVI, Num 1, pp. 10-18
- Chelén-Franulic, J., 1987, Difracs, Modelo de Deformación de Campo Físico, Geología Estructural: Memorias Trabajos Técnicos XVII Convención Nacional A.I.M.M.G.M AC
- Gómez-Marín, E., 1995, Esto es el Caos, Primera Edición, ADN Editores, México
- Hobbs, B., Means, W., Williams, P., 1976, An Outline of Structural Geology, Wiley Press, N.Y.
- Mandelbrot, B, 2014, El Fractalista, Memorias de un científico inconformista, Primera Edición en Metatemas, Tusquets Editores, México.
- Martínez-Mendoza, J.A., 1995, Perspectivas de nuevos depósitos con base en un arreglo estructural caótico en el distrito Guanajuato, Resumen Trabajos Técnicos XXI Convención Nacional, AIMMGM.
- McCoss, A., 1986, Simple constructions for deformation in transpression/transtension zones, Journal of Structural Geology, Vol. 8, No. 6, pp.715-718
- Mejía, P.E., 1987, Difracs: Modelos Matemáticos Aplicados a Geología: Resumen Trabajos Técnicos XVII Convención Nacional, A.I.M.M.G.M. AC.
- Navarro-Yañez, A., 2014, El Científico que derrotó a Hitler y otros ensayos sobre la historia de la ciencia, Primera Edición, Editorial Almuzara, Barcelona, España.
- Ortiz-Hernández, L.E., Escamilla-Casas, J, Acevedo-Sandoval, O., 2005, Distribución y tipología de depósitos auríferos en México, Memorias Trabajos Técnicos, XXVI Convención AIMMGM.
- Pérez-Reverte, A, 2006, El pintor de batallas, Quinta reimpresión 2013, Editorial Alfaguara, México.
- Ragan, D.M., 2009, Structural Geology, an Introduction to Geometrical Techniques, Fourth Edition, Cambridge University Press.
- Ruiz-Gutiérrez R. y Ayala F.J., 2004, El Método en las Ciencias, Epistemología y darwinismo, Sección de Obras de Ciencia y Tecnología, Fondo de Cultura Económica.
- Ruiz, M., Fernández, T. y Tamaro, 2004, Biografías y Vidas. La enciclopedia biográfica. Barcelona (España).
- Schifter, I, 1996, La Ciencia del Caos, La ciencia desde México, Fondo de Cultura Económica.
- Singer, D., Berger, V., Moring, B., 2002, Porphyry Copper Deposits of the world: database, maps and preliminary analysis, USGS.
- Talanquer V., 1996, Fractus, Fracta, Fractal, fractales, de laberintos y espejos, La Ciencia desde México, Fondo de Cultura Económica, México.
- Yacamán, M., 1994, El Caos, la nueva física, las nuevas matemáticas y sus aplicaciones a las ciencias sociales., Revista Ciencia y Desarrollo, CONACYT, Vol. XIX, No.114
- 1 Consultor en Geología Económica/geo.jamm@icloud.com
- 2 Ruiz R. y Ayala F.J., 2004, El Método en las ciencias, Fondo de Cultura Económica, p.45
- 3 Diccionario virtual de la Real Academia de la Lengua Española.
- 4 Ruiz M., Fernández, T. y Tamaro, 2004, En Biografías y Vidas. La enciclopedia biográfica, Barcelona (España).
- 5 Ibidem.
- 6 Schifter, I, 1996, La Ciencia del Caos, La ciencia desde México, Fondo de Cultura Económica, p.11
- 7 Arenas, J, 2014, ¿Es estable el Sistema Solar?, Lat. Am. J. Phys. Educ. Vol. 8, No. 2, June, pp.329-330
- 8 www.astrofisicayfisica.com/2014/04/la-relatividad-general.html
- 9 Schifter, I, 1996, ibid, p.14
- 10 Ibidem p.11
- 11 Navarro-Yañez, A., 2014, El Científico que derrotó a Hitler y otros ensayos sobre la historia de la ciencia, Primera Edición, Editorial Almuzara, Barcelona, España. P.187
- 12 Sensibilidad especial para captar ciertas radiaciones, utilizada por los zahoríes para descubrir manantiales subterráneos, venas metalíferas, etc., Diccionario Real Academia de la Lengua Española.
- 21 Camprubi, A., González-Partida, E., Levresse, G., Tritlla, J., Carrillo-Chávez, A., 2003, Depósitos epitermales de alta y baja sulfuración: una tabla comparativa, Boletín de la Sociedad Geológica Mexicana, Tomo LVI, Num 1, pp. 10-18
- 22 Martínez-Mendoza, J.A., 1995, Perspectivas de nuevos depósitos con base en un arreglo estructural caótico en el distrito Guanajuato, Memorias de la XXI Convención Nacional, AIMMGM.
- 23 Braun, E., 1999, Caos, fractales y cosas raras, Segunda Edición La Ciencia para todos, Fondo de Cultura Económica, pp.11-12
- 24 Talanquer, V., Ibid., P.25
- 25 Ibidem, p.25
- 26 Mandelbrot, B, 2014, El Fractalista, Memorias de un científico inconformista, Primera Edición en Metatemas, Tusquets Editores, México. pp.161-165
- 27 Mandelbrot, B., 2014, pp. 273-274
- 28 Ibidem, p.323


















