/ LEER MÁS leer mas
Ediciones en PDF GEOMIN.COM.MX

Simulación fractal usando sistemas de funciones iteradas en geología: En el ejemplo del gabro del cerro El Chalio, Coahuila, México

Por: 1Karla Rosalyne Lira Méndez, 1Alberto Hernández Rosales, y 1Roberto Díaz Martínez.

Resumen
En este trabajo de investigación, se hace una simulación de un fractal natural, correspondiente a una muestra de gabro perteneciente al cerro El Chalio, ubicado al norte del estado de Coahuila de Zaragoza, México. Para la simulación se usan sistemas de funciones iteradas; el proceso es realizado con ayuda del software IFS Construction Kit, un software de iteración aleatoria. El resultado obtenido se presenta en la Figura 5. Este resultado es una primera aproximación, se pueden obtener más alterando las transformaciones contractivas dadas en la Tabla 2. 

Palabras clave: fractales, simulación, geología, sistemas iterados, transformaciones contractivas.

Abstract
In this research work, we are presenting the result of the simulation of a natural fractal, corresponding to a sample of gabro belonging to the Chalio hill, located in the north of the state of Coahuila de Zaragoza, Mexico.  For the simulation, we used iterated function systems; the iterative process was carried out with the help of IFS Construction Kit software. The result obtained is presented in Figure 5. This result is a first approximation, more can be obtained by altering the contractive transformations of Table 2.

Key words: fractals, simulation, geology, iterated systems, contractive transformations.

Introducción
Mandelbrot (1967) llama “fractal” a objetos geométricos cuya estructura es irregular. Según Mandelbrot, la palabra fractal proviene del latín fractus, que significa “quebrado o fracturado”, del verbo frangere, “romper”. En la actualidad, se tiene la siguiente clasificación: fractales lineales, no lineales y fractales autoafines o naturales.

La geometría fractal es reciente en la matemática, su desarrollo se ha acelerado debido a su diversidad de aplicaciones en diferentes campos de la ciencia y la tecnología, gracias al desarrollo informático (González et al., 2019). Algunos ejemplos de formas naturales son: los perfiles costeros, la hoja de un helecho, las fronteras de los paisajes, la superficie rugosa de una roca, el ramaje de un arbusto, la ramificación alveolar en los pulmones, la frontera de una nube y las fluctuaciones de precios en un mercado (Talanquer, 2011). En la actualidad, la geometría fractal es muy aplicada en la física, medicina, computación, química, biología, economía, fisiología, arte, etc. ya que ha permitido reformular y resolver problemas complejos de una forma muy simplificada (Alfaro et al., 2010).

En todos los objetos naturales o fractales afines a los que se ha hecho referencia en el párrafo anterior, se ha usado el concepto de escala o escalado. Según Gumiel (1996) una de las percepciones físicas clave en la definición conceptual de un fractal, es que todo proceso u objeto muestra características semejantes a diferentes escalas, por consiguiente, es invariante al cambio de escala. Estas propiedades siguen distribuciones hiperbólicas, donde la propiedad (P) está relacionada con el tamaño (t) mediante la ecuación P= Ct -D,D es la dimensión fractal del sistema, la cual se obtiene de la siguiente manera (Gumiel, 1996):

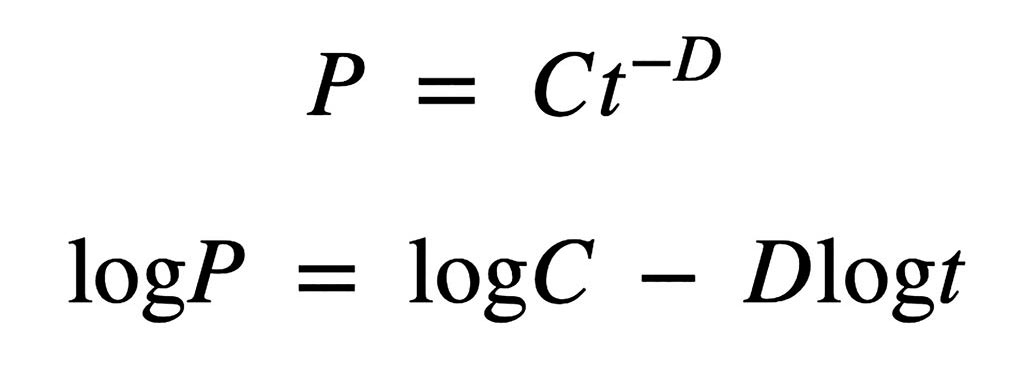
por lo tanto,

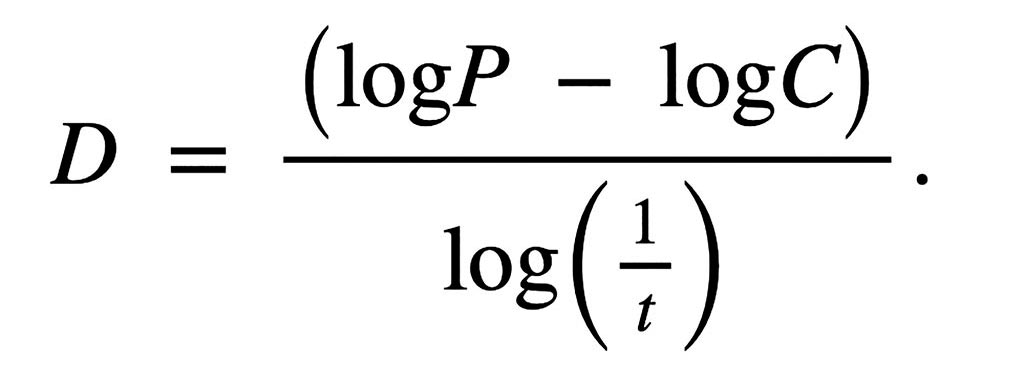
La ecuación anterior cuantifica el grado de irregularidad y fragmentación de un conjunto geométrico, o un sistema geológico, u objetos naturales.

En la naturaleza son más frecuentes los fractales autoafines, aquellos en los que el objeto es parecido a diferentes escalas, pero no como un calco (fractales naturales o autoafines) (Barnsley, 1988).

Gumiel (1996) menciona que en geología el concepto de fractal se empezó a usar principalmente en los campos de Geomorfología y Sismología, cuando en la zona de la Falla de San Andrés en California, E.U., se descubrió que los sismos de magnitud 6 o menor tenían una distribución fractal en el espacio y en el tiempo. Al comprobar que los temblores se presentaban en grupos autosemejantes y no en intervalos regulares.

Existen varias aplicaciones de fractales en la geología, algunas de estas son las siguientes: Turcotte (1986) comprobó que las relaciones tonelaje – ley de algunos yacimientos de Hg, Cu y U de Estados Unidos presentaban también distribuciones fractales. Análisis cartográfico de la dimensión fractal para la variación espacio-temporal de ríos (González et al., 2019). Uso del modelo fractal para caracterizar la distribución de tamaño de partícula en suelos (Filgueira et al., 2002). En el caso de Hernández et al. (2021) estudian las relaciones de las características geológicas y la dimensión fractal de las Sierras de Obayos y Santa Rosa, del estado de Coahuila, México. Estimación de la distribución geométrica de fallas en macizos rocosos (Moná et al., 2019). Y finalmente, Hernández et al. (2023) estudian las relaciones de las características geológicas y la dimensión fractal de afloramientos rocosos ubicados en Melchor Múzquiz, Coahuila, México.

Por otro lado, existen trabajos relacionados con el uso de sistemas de funciones iteradas para la generación de fractales autoafines. Algunos son los siguientes: en (Barnsley y Demko, 1985) usan la teoría de sistemas de funciones iteradas para generar diversos fractales autoafines y fractales matemáticos. En (Hodges y Naylor, 1985) también se usan sistemas de funciones iteradas para crear objetos fractales como gráficos de interpolación fractal, hojas de Arce, hojas de Arce Alicatada, y hojas de helecho.

En este sentido, se puede apreciar que es posible aplicar la geometría fractal a través de sistemas de funciones iteradas para crear distintos objetos fractales vinculados con formaciones geológicas. Por esta razón, en la presente investigación se realiza una simulación de una muestra de gabro perteneciente al cerro El Chalio, ubicado al norte del estado de Coahuila, México; usando Sistemas de Funciones Iteradas. Esto se justifica porque a simple vista en la muestra de gabro se puede observar distribuciones que se repiten a diferentes escalas, característica fundamental de los fractales afines.

Descripción geológica y ubicación de la muestra de gabro
La imagen que se presenta en la Figura 1 corresponde a una muestra de gabro natural, dicha estructura atiende características fractales naturales. Para atender el objetivo de esta investigación, la imagen de la Figura 1 será simulada usando sistemas de funciones iteradas con la ayuda del software IFS Construction Kit.

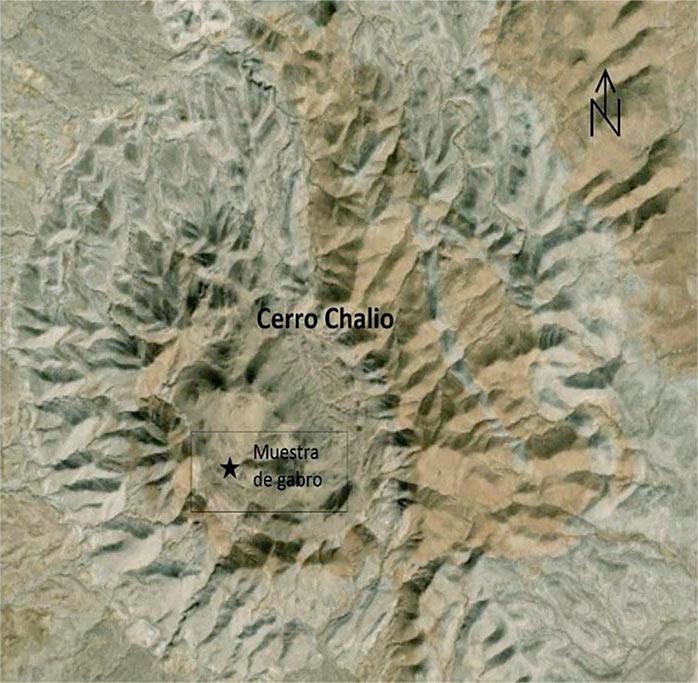
La muestra objeto de estudio se recolectó en un afloramiento de rocas ígneas perteneciente al cerro El Chalio, ubicado al norte del estado de Coahuila. Sus coordenadas UTM son las siguientes: X=707429; Y=3190445 (Figura 2).

 Esta roca se describió petrográficamente con ayuda de un microscopio de luz polarizada marca Leica, definiéndose como un gabro de grano grueso, de color oscuro muy fresco en la que se observa plagioclasa (Pl) euhedral con las características ópticas de la labradorita, abundante titanoaugita (Ti-Aug) y olivino (Ol); este último, atendiendo a su muy alto relieve, color y pleocroísmo parece ser fayalita o un olivino muy rico en hierro. Es común observar al olivino incluido dentro de grandes cristales de titanoaugita (Figura 3).  

Figura 1. Fotografía del gabro pulido perteneciente al cerro El Chalio, Coahuila.
Figura 2. Cerro Chalio, ubicación satelital.
Figura 3. Microfotografía del gabro del cerro El Chalio. a) Se observa cristales de plagioclasa alargados euhedrales incluidos dentro de la titanoaugita. b) La misma imagen con nicoles cruzados.

Sistemas De Funciones Iteradas
Definición 1.
Sea ( X,d) un espacio métrico. Se denota con F (X), la familia de todos los subconjuntos compactos no vacíos de X, es decir:

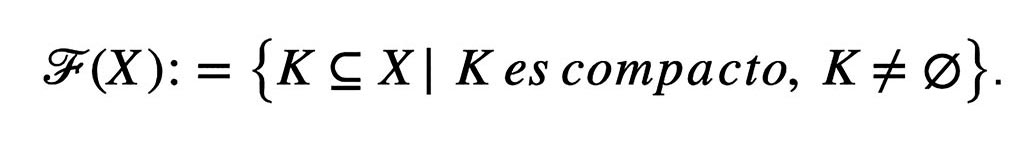
Definición 2. 
Sea ( X,d) un espacio métrico, sean 
Se define la distancia de x al conjunto A como

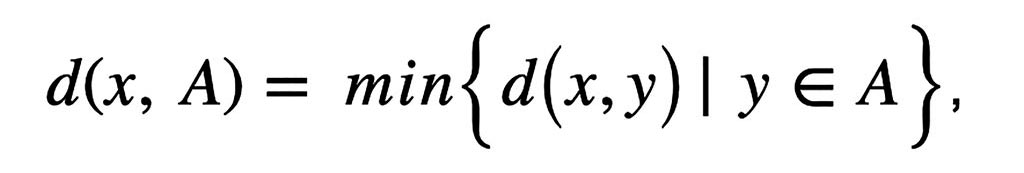
y la distancia de (Figura 4), para más información sobre las definiciones anteriores consultar (Iribarren, 2008).

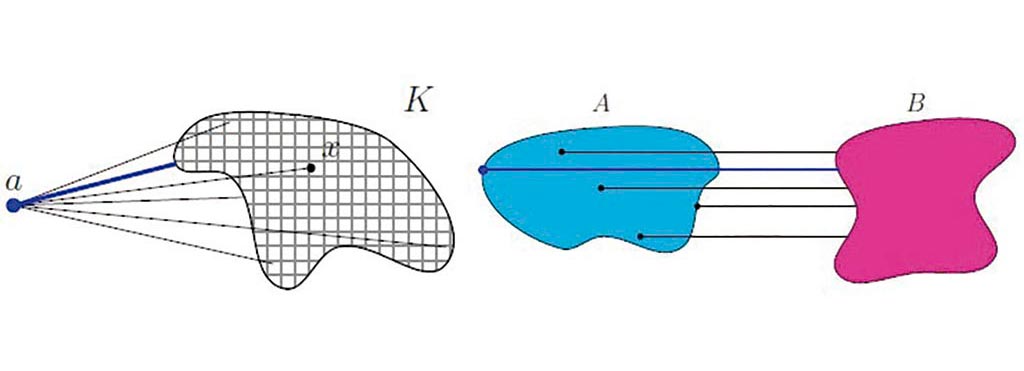
Figura 4. Distancia de un punto αεX a un conjunto compacto K y la distancia entre compactos A y B. Fuente: (Sabogal y Arenas, 2011).

Proposición 1. Sea (X,d) un espacio métrico, y sea 
la función que se define como:  

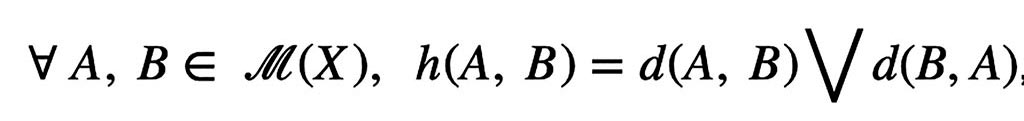
, entonces h es una métrica sobre (X) .

Para más información sobre la Proposición 1, consultar (Iribarren, 2008).

Teorema 1. Sea (X,d)  un espacio métrico completo, entonces el espacio métrico (  (X),h ) es completo.

La demostración del Teorema 1 se puede consultar en (Iribarren, 2008).

El espacio métrico antes mencionado también es conocido como métrica de Hausdorff.

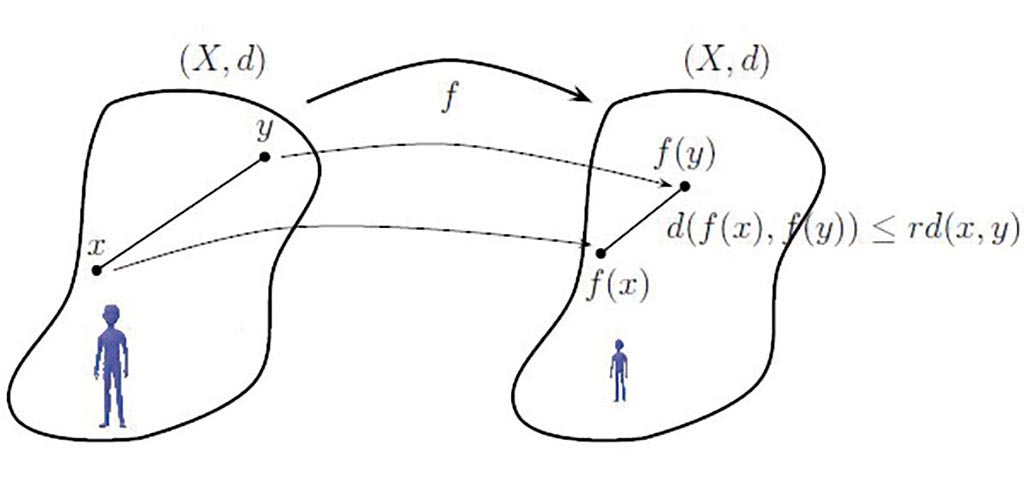
Definición 3. Sean (X1,d1)  y (X2,d2) dos espacios métricos. Una función   f: (X1,d1) → (X2,d2)  es una función de Lipschitz, si existe un número real positivo α tal que

 ,

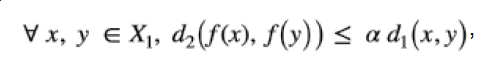
al número α se le llama un factor de Lipschitz de la función f . Si se cumple que 0 ≤ α < 1, entonces f es llamada una contracción y α un factor de contracción para f (Figura 5).

Figura 5. Notación intuitiva de función contractiva. Fuente: (Sabogal y Arenas, 2011).

Teorema 2. (Teorema del punto fijo). Si (X, d) es un espacio métrico completo y f: X → X una contracción, con α un factor de contracción de f, entonces existe un único xf X tal que f(xf)= xf, a xf se le llama el punto fijo de la contracción. Para más información revisar (Mahanta, 2018).

Sistemas de funciones iteradas
Proposición 2.  Sea (X, d) un espacio métrico completo y sea para i{ 1, . . . , n },  fi: (X,d) → (X, d) contracciones con αi un factor de contracción para fi. Sea F:(  (X), h) →( (X),h) la función definida por 

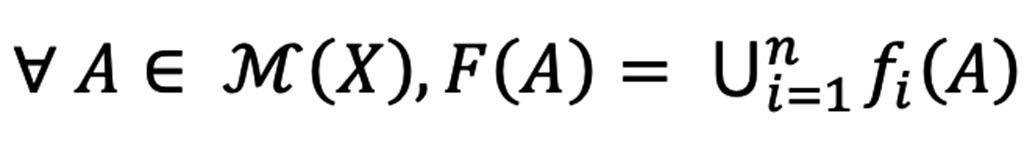
entonces F es una contracción y α=máx { αi | i {1, . . . , n}} es un factor de contracción para F. Para más información sobre la Proposición 2, véase (Mahanta, 2018).

Definición 4. Un sistema de funciones iteradas o SFI, consiste de un espacio métrico completo y una familia finita de contracciones { fi: (X,d) → (X, d)|i {1, . . . , n}}, al SFI se le denota por {(X, d); f1, f2, f3, …, fk }, y se llama un factor de contracción del SFI al número α= máx{αi| i{1, . . . , k}}, donde el númeroαi es un factor de contracción para fi, i{1, . . . , k}.

Más información sobre la Definición 4, se puede encontrar en (Mahanta, 2018).

De acuerdo con la Proposición 2, dado un sistema de funciones iteradas {(X, d); f1, f2, f3, …, fk}, se puede definir una contracción F en el espacio métrico completo ( (X), h), y por el Teorema 2 existe un único AF(X), tal que este es el punto fijo de la contracción, el conjunto AF es llamado el conjunto fractal asociado al SFI y a F la contracción inducida por el SFI, véase (Juárez y Correa, 2012).

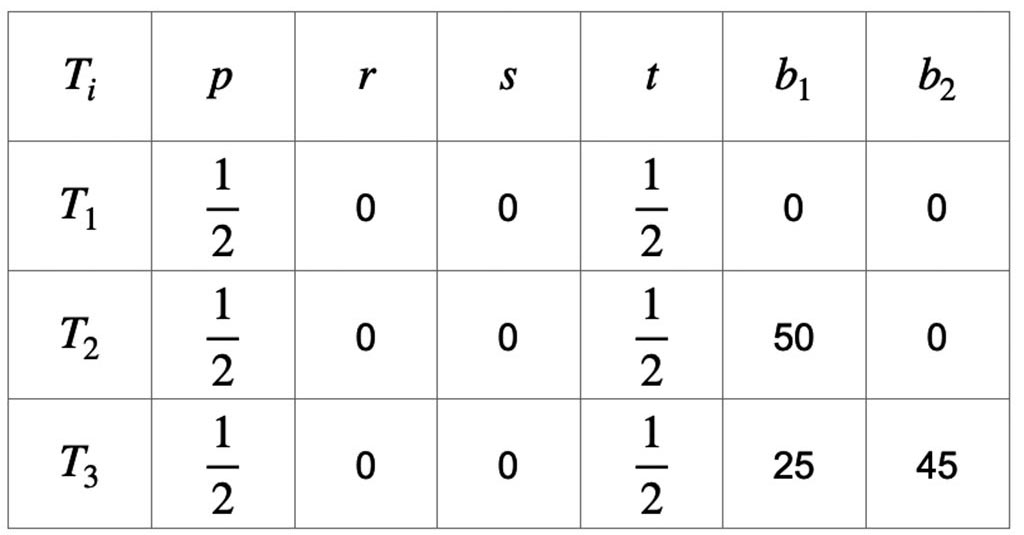
En la Tabla 1 se tiene un ejemplo de un sistema de funciones iteradas para generar el fractal lineal conocido como triángulo de Sierpinsky.

Usando el software IFS Construction Kit y las transformaciones afines de la Tabla 1 que conforman el sistema de funciones iteradas, se obtiene el fractal de la Figura 6. Éste fue calculado con 281,100 puntos de resolución.

Tabla 1: Transformaciones afines para generar el Triángulo de Sierpinsky.

Para generar la simulación de la muestra de gabro perteneciente al cerro El Chalio, ubicado al norte del estado de Coahuila, México, se usa el software IFS Construction Kit, el cual hace uso de un algoritmo aleatorio, y usa sistemas de funciones iteradas, véase (Barnsley, 1988) y con la ayuda de las transformaciones contractivas de la Tabla 2.

Figura 6: Triángulo de Sierpinsky construido. Creación propia.

Resultados y discusión
El resultado de la iteración del sistema de funciones iteradas mediante el software IFS Construction Kit, se puede apreciar en la Figura 7. Esta imagen se obtiene de acuerdo con el sistema de funciones iteradas dado en la Tabla 2.

La simulación tiene 1,000,000 de puntos de resolución.

Se debe mencionar que la imagen presentada en la Figura 7 no es única, porque si se alteran las transformaciones afines dadas en la Tabla 2 resultaría una imagen totalmente diferente. Por lo que se debe tener cuidado al elegir las transformaciones contractivas. Lo que conocemos como teoría del caos en matemáticas, se hace presente en este proceso al cambiar los datos de las transformaciones afines.

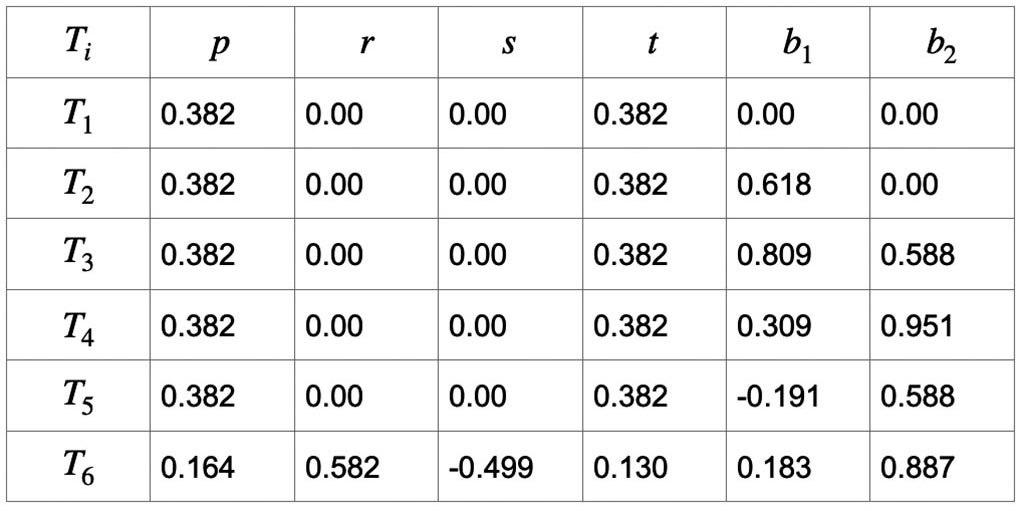
Tabla 2. Transformaciones afines que generan la simulación de gabro.
Figura 7. Simulación de la muestra de gabro usando el sistema de 
funciones iteradas de la Tabla 2.

La geometría fractal hoy en día es la única herramienta capaz de crear simulaciones de objetos naturales, con un nivel de precisión muy alto, véase (Gumiel y Hernández, 1996), (Álvarez, 2021) y (Juárez y Correa, 2012). Y si se desea estudiar la forma de los objetos o sistemas geológicos naturales, se tiene que recurrir forzosamente a la geometría fractal para poder tener acceso a su forma física.

Conclusiones
La geometría fractal presenta una nueva geometría de la naturaleza y ofrece una nueva herramienta poderosa para abordar estudios geométricos de sistemas naturales complejos. La geometría fractal nos ofrece la posibilidad de comprender las leyes que gobiernan dichos sistemas y en un futuro obtener mediante el desarrollo de los ordenadores, modelos matemáticos que ayuden a predecir el comportamiento de sistemas dinámicos naturales. 

Referencias

  1. Alfaro, M., Murillo, M. y Soto, A., 2010, Fractales, Primera edición, Costa Rica: Ed. Revista digital matemática educación e internet, 87 Pp.
  2. Álvarez, Y., 2021, Sistema de Funciones Iteradas, Fractales y Multifractales [Tesis de maestría]. Universidad Autónoma Metropolitana. https://bindani.izt.uam.mx/concern/file_sets/wh246s331?locale=es.
  3. Barnsley M. F., 1988, Fractals everywhere, Academic Press, Inc. 394 p.
  4. Barnsley, M. F. & Demko, S., 1985, Iterated Function and the Global Construction of Fractals. Proceedings of the Royal of London. Series A, Mathematical and Physical Sciances, Volumen 399, Issue 1817 (Jun. 8, 1985), 243-275. 
  5. Filgueira, R., García, M., Roggiero, M., Aragón, A. y Sarli, G., 2002, Uso del modelo fractal para caracterizar la distribución de tamaño de partículas en suelos. Ciencia del Suelo. 20 (2): 114-117.
  6. González, H., Argüeyes, L. y Álvarez, M., 2019, Análisis cartográfico de la dimensión fractal para la variación espacio temporal de ríos. Revista Geoespacial. 16 (1): 78-97.
  7. Gumiel, P., 1996, Fractales, su importancia en geología. Simulación de patrones fractales naturales, Geogaceta, 20 (6), 1382-1384.
  8. Gumiel P. y Hernández, R., 1996, Simulación de Patrones de Fracturación en Roca, Distribución y Características de su Geometría Fractal. Conectividad y Percolación, Geogaceta, 20 (6), 1409-1412.
  9. Hernández, A., Almaguer, Y., Díaz, R., Lira, K., López, F. y Valdés, A., 2021, Dimensión fractal de las redes de drenaje superficial de las Sierras de Obayos y Santa Rosa, Coahuila. Ciencia Cierta. 67: 146-169.
  10. Hernández, A., Almaguer, Y., Lira, K., Díaz, R., López, F., Briseño, H. y Martínez, R., 2023, Dimensión fractal de macizos carbonatados naturalmente. Ejemplo de la formación aurora, noreste de México. CienciAcierta. 75: 183-218.
  11. Hodges, L., and Naylor, B., 1985, Construction of fractal objects with Iterated Function Systems. SIGGRAHP ’85. 19: 271-278.
  12. Iribarren, I., 2008, Topología de espacios métricos. Limusa, 253 Pp.
  13. Juárez, S. M. y Correa, F. M., 2012, Sistemas de funciones iteradas por partes. Morfismos, Vol. 16, 1, 9-27.
  14. Mahanta, A., Sarmah, K. and Choudhury, G., 2018, Iterated function systems as a generator of fractal objects. International Journal of Creative Research Thoughts, Volume 6, 123-142.
  15. Mandelbrot, B., 1967, How long is the coast of Britain? Statistical self-Similarity and fractional dimension. Science, New Series. 156, (3775), p. 636-638.
  16. Moná, J., Echeverri, R. y Brasil, A., 2019. Aplicación de la teoría fractal para la estimación de la distribución geométrica de fallas en macizos rocosos [Tesis de Maestría, Universidad Nacional de Colombia]. https://repositorio.unal.edu.co/handle/unal/77499?show=full
  17. Sabogal, S. y Arenas, G., 2011, Una introducción a la geometría fractal. [En línea]. Disponible en: http://matematicas.uis.edu.co/libros/l_geofrac.pdf. Fecha de consulta: 20 de mayo de 2022.
  18. Talanquer, V., 2011, Fractus, fracta, fractal, fractales de laberintos y espejos. México: Ed. Fondo de cultura económica. 114 pp.
  19. Turcotte, D. L., 1986, A Fractal Approach to the Relationship between Ore Grade and Tonnage, Economic Geology. 81, p. 1528-1532.

1.Universidad Autónoma de Coahuila, Escuela Superior de Ingeniería “Lic. Adolfo López Mateos”. Boulevard Adolfo López Mateos s/n. Nueva Rosita, Coahuila, México. C P. 26800. karla.lira@uadec.edu.mx.