Evaluación del consumo energético en la fractura por compresión en mineral de calcopirita (CuFeS2)
Por: R. Rodríguez1, *G. Rosales1, G. Alvarado1, J. Andrade1 y E. Espinosa1
Resumen
La trituración es un paso esencial en el procesamiento de mineral debido a que antecede a la molienda. En este proceso se rompe el mineral de la mina a fin de exponer las partículas valiosas que se recuperarán en otros procesos. Existen tres mecanismos básicos empleados para reducir el tamaño del material: impacto, abrasión, y compresión. El material triturado por compresión por lo general presenta tensiones internas que pueden causar un subsecuente agrietamiento; esto se traducirá en un decremento de la cantidad de energía en el proceso de molienda. Existen reportes de que la fractura en cama de partículas producida en el molino de rodillos a alta presión tiene potencial para mejorar la liberación de minerales a través de una fractura preferencial, ya que aprovecha las pequeñas imperfecciones microscópicas en la masa del mineral, conocidas como grietas de Griffith. En este trabajo un mineral CuFeS2 cuya densidad es de 2.38 g/cm3 fue usado. Este tipo de mineral tiene una dureza de 4 en la escala de Mohs. La distribución granulométrica a monotamaño (-19 mm + 12,5 mm) se preparó a partir de un muestreo en planta, donde se obtuvieron 572.3 kg de muestra. El pistón diseñado para el trabajo experimental tuvo un diámetro (D) de 0.125 m y una altura (h) de 0.075 m. Una máquina de tensión universal de 600kN fue usada para fracturar el mineral en lecho comprimido. Para determinar la energía el gráfico esfuerzo versus deformación fue empleado, posteriormente los Joules fueron convertidos en términos de energía especifica (kWh/ton). El Índice de trabajo de trituración fue determinado acorde con lo estipulado con Frederick C. Bond resultando en 8.3 kWh/ton, se demostró que el consumo de energía por compresión fue de 0.986 kWh/ton.
Palabras clave. Compresión de partículas, consumo de energía, trituración y molienda.
Abstract
Crushing is an essential step in mineral processing, this operation precedes milling. In this process the ore is broken in the mine, to expose the valuable particles that are recovered in other processes. There are three basic mechanisms used to reduce the size of the material: impact, abrasion, and compression. Crushed material by compression usually presents internal stresses that can cause subsequent cracking; This will result in a decrease in the amount of energy in the grinding process. There are reports that the fracture in the particle chamber produced in the high-pressure roller mill has the potential to improve the release of minerals through a preferential fracture, since it takes advantage of small microscopic imperfections in the mass of the ore, known as Griffith cracks. In this work, a CuFeS2 mineral whose density is 2.38 g / cm3 was used. This type of mineral has a hardness of 4 in Mohs scale. The granulometric distribution to single size (-19 mm + 12.5 mm) was prepared from a plant sample, where 572.3 kg of sample was obtained. The piston designed for the experimental work had a diameter (D) of 0.125 m and a height (h) of 0.075 m. A universal tension machine was used to fracture the mineral in compressed bed until 600kN. To determine the energy the stress versus strain graph was used, energy expressed in joules were converted in terms of specific energy (kWh/ton). The crushing work index was determined in accordance with the stipulated with Frederick C. Bond resulting in 8.3 kWh/ton, it was demonstrated that the energy consumption by compression was 0.986 kWh/ton
Keywords. Piston press die, energy consumption, crushing and grinding
Introducción
Fractura por compresión en cama de partículas
El proceso de fractura por compresión de partículas comenzó a ser estudiado por Schönert en 1988. Su uso y principal aplicación fue para la industria del cemento, pero recientemente se han hecho estudios para evaluar la factibilidad de procesar minerales.
En la fractura de partículas con lecho confinado, las partículas son sometidas a múltiples fuerzas de contacto debido a las partículas vecinas y el efecto de la pared sólida. Las simulaciones numéricas de lechos de partículas comprimidas han demostrado que el esfuerzo de compresión promedio dentro de las partículas, es comparable con la tensión aplicada en la superficie de la cama de partículas; sin embargo, la tensión en los puntos de contacto puede ser varias veces mayor (Djordjevic y Morrison, 2006). Cuando la tensión inducida alcanza la resistencia de la partícula, la partícula falla. En este contexto, la fractura entre partículas en confinamiento ha sido investigado numéricamente desde el punto de vista de la mecánica (Liu et al., 2014). Se ha encontrado que la fragmentación se inicia a partir de las partículas que están sometidas a esfuerzos de compresión quasi-uniaxial, donde la partícula asimila el esfuerzo en zonas diametralmente opuestas, por lo que se produce una división axial muy pequeña. Después de eso, las partículas debido al confinamiento y la interacción con partículas vecinas reciben esfuerzos amplificados en los puntos de contacto entre ellas y da origen a la fractura en los planos cristalinos. Con el tiempo, la compresión local en los puntos de contacto se convierte en un mecanismo importante de falla. En un lecho comprimido de partículas con distintos tamaños, las partículas relativamente más pequeñas tienen menos puntos de contacto y están bajo una compresión cuasi-uniaxial y, por lo tanto, la fragmentación se inicia desde la partícula más pequeña. Las partículas más gruesas son más difíciles de romper ya que en los espacios intersticiales muy pocas partículas pequeñas se encuentran ocluidas, lo que disminuye los puntos de contacto. Las simulaciones numéricas han demostrado también que la fractura dentro de un lecho de partículas comprimido progresará desde la superficie de trituración hacia la profundidad de la cama, donde se produce la más alta compactación y la porosidad más baja (Djordjevic y Morrison, 2006).
Hasta cierto punto, el enfoque de la prensa de prueba pistón ha sido estandarizada por Schönert (1996), donde se establecieron las pautas geométricas para la investigación de la fractura entre las partículas a través de una serie sistemática de pruebas de fractura por medio de compresión. Sin embargo, los efectos de la pared en esta prueba son significativos por lo que la geometría debe especificarse cuidadosamente. La geometría apropiada del lecho de material en la matriz se define según la Ecuación (1):
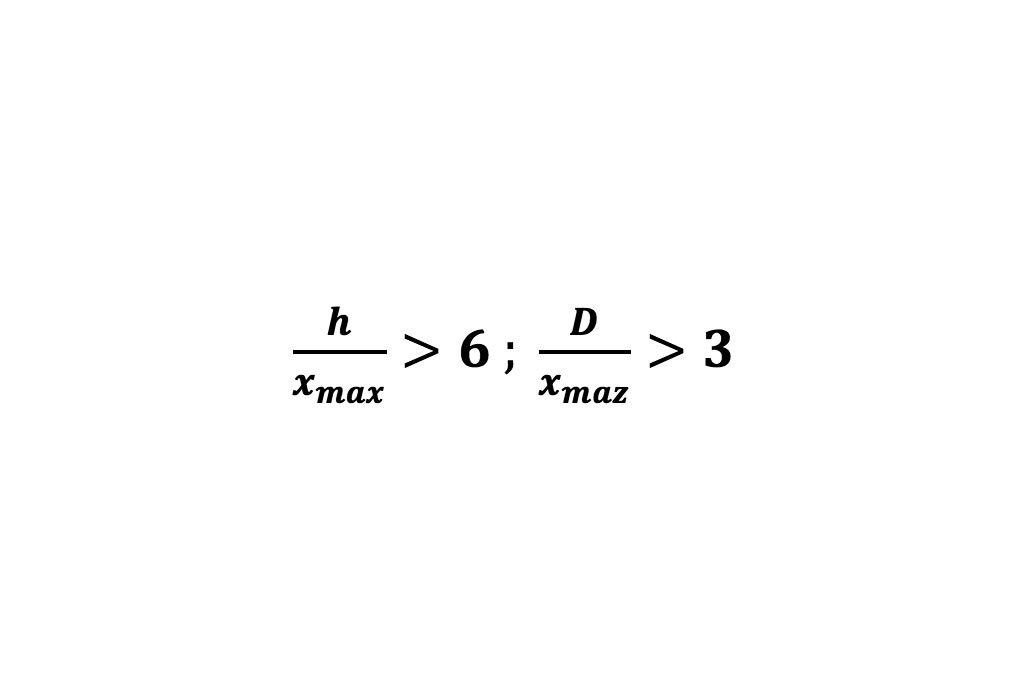
(1)
Estudios de compresión en pistón, incluyendo el de Daniel; (2002), Oettel et al., (2004), y Hawkins (2007), han utilizado esta guía como base para las pruebas de pistón de prensa (Ecuación 1). De esta manera el material a comprimir en el pistón permite al operador especificar directamente la presión aplicada a la cama de material.
Un enfoque convencional ha sido traducir la energía específica consumida durante una prensa de pistón para un valor específico de energía. La energía específica consumida durante un ciclo de prensa de pistón se puede determinar a través de la integración de la curva del gráfico esfuerzo contra desplazamiento, dando como resultado unidades de trabajo (o de potencia si se observan unidades de tiempo). Este enfoque ha demostrado ser el principal método de comparación de energía específica consumida de la prensa de pistón, y fue incluido en estudios como el de Fuerstenau et al. (1996), Oettel et al. (2004), Daniel (2002), Hawkins (2007) y Bulled et al. (2009).
Metodologia experimental
El mineral usado en esta prueba fue una mena de CuFeS2 cuya densidad es de 2.38 g/cm3. Este tipo de mineral tiene una dureza de 4 en la escala de Mohs. El material fue ensayado para determinar el consumo energético (kWh/t) aplicando el índice de trituración de F. Bond. Posteriormente, el mineral fue ensayado usando una máquina universal de tensión y un pistón.
Prueba de indice de trituracion de Bond
El equipo para el ensayo de impacto desarrollado por Bond es utilizado por los principales fabricantes de quebradoras. La prueba se realizó con una serie de 10 a 50 partículas del mineral propuesto (CuFeS2). El espesor de la roca fue un monotamaño de (-19 mm + 12,5 mm). La resistencia al impacto de la roca en pie-lb por pulgada de espesor se designa como KC y el índice de trabajo, en kWh/t, se calcula como el promedio de 10 rupturas según la Ecuación 2:
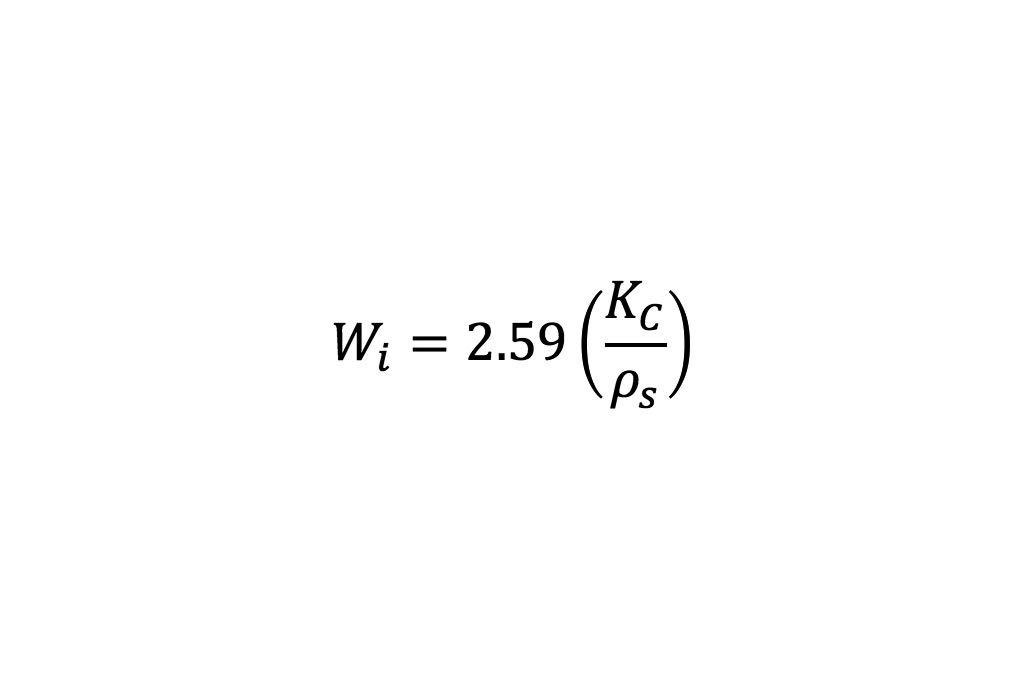
(2)
donde ρs es la gravedad específica de la roca.
Pruebas de compresion en pistón
La distribución granulométrica a monotamaño (-19 mm + 12,5 mm) se preparó a partir de un muestreo en planta. El pistón diseñado para el trabajo experimental tuvo un diámetro (D) de 0.125 m y una altura (h) de 0.075 m. La Ecuación 1 define la relación entre h y D, y los datos experimentales se muestran en la Tabla 1.
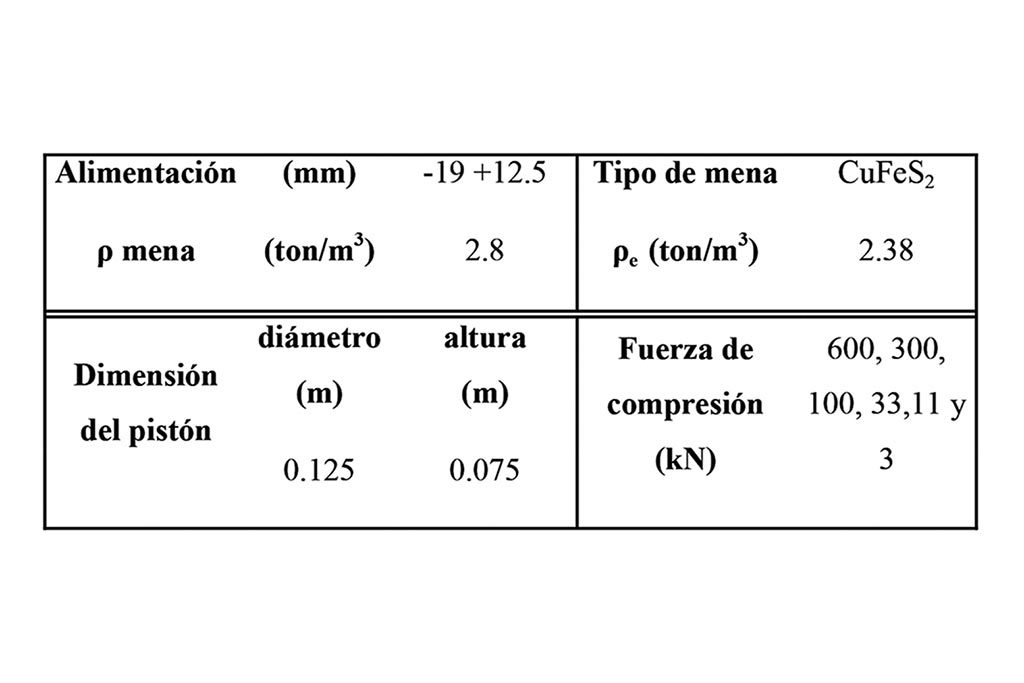
La Figura 1 muestra las dimensiones del pistón y de la máquina universal de tensión utilizados. La prensa tiene una capacidad máxima de 600 kN, la cual está conectada a un ordenador de control que registra los datos del gráfico esfuerzo contra deformación durante la prueba. Las cinéticas de compresión fueron realizadas con una velocidad constante del cabezal de 0.05 m/min; el límite propuesto fueron los esfuerzos de 600, 300, 100, 33, 11 y 3 kN, los cuales se alcanzaron en un tiempo de 1.5, 0.75, 0.25, 0.083, 0.027, y 0.009 min. respectivamente.
Para las pruebas cinéticas de compresión el volumen de la matriz fue calculado, y la muestra mineral fue insertada en la hembra del pistón. La distancia entre el pistón y la matriz fue medida antes de realizar la prueba (0.75 mm). El pistón con el mineral se colocó en la máquina de tensión universal para comenzar el proceso de compresión. Los parámetros de control se expresaron en kN/mm2 para la fuerza máxima; el período de tiempo en el que se mantiene la fuerza máxima se expresa en segundos. La cantidad de energía administrada durante la carga y la cantidad de energía liberada durante la descarga se calcula a partir de la curva de esfuerzo deformación.

Después de completarse la prueba de compresión se midió la distancia entre la parte superior del pistón y la parte superior de la matriz, de modo tal para calcular el espesor y el contenido de sólidos del material compactado; conociendo el volumen final y la cantidad de masa, la densidad del compactado de partículas fue calculada.
Resultados y discusiones
Determinación de Índice de trituración
La Tabla 2. muestra los resultados para la obtención del índice de trituración de Bond. Para este caso un total de 20 partículas fueron ensayadas de acuerdo con la metodología descrita con anterioridad.
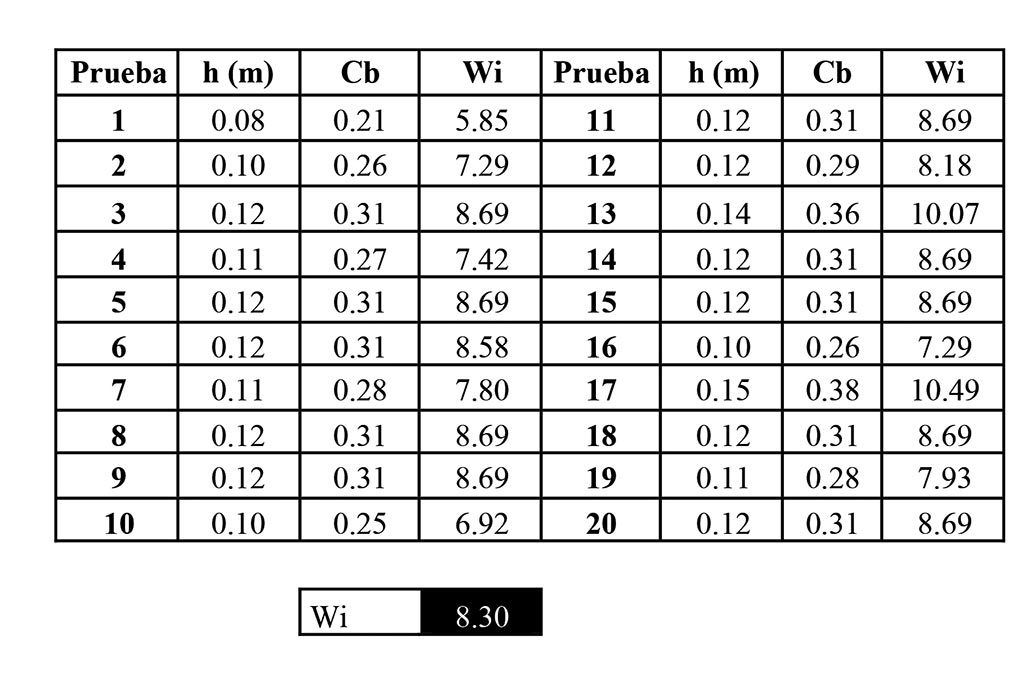
Usualmente, los ensayos de trituración para muestras minerales suelen ser de menor magnitud que aquellos que son de molienda. Cabe resaltar que esta prueba tiene como mecanismo principal el impacto, este mecanismo genera un tamaño de partícula con menor cantidad de partículas finas como se muestra a continuación en el gráfico de la Figura 2.
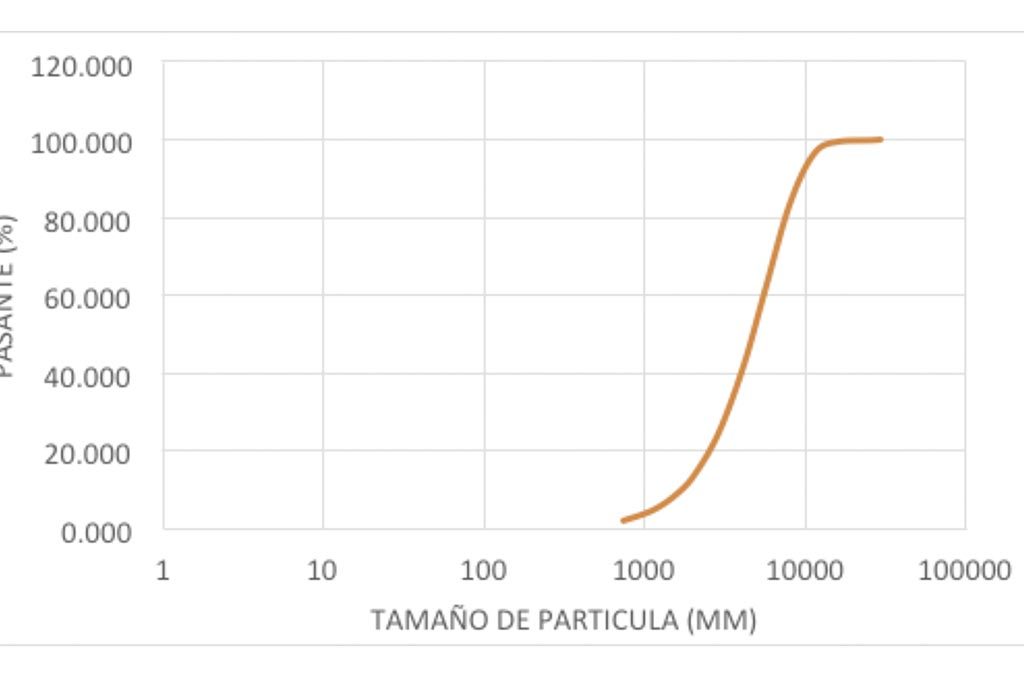
(Índice de Trituración de Bond)
Compresión de partículas confinadas
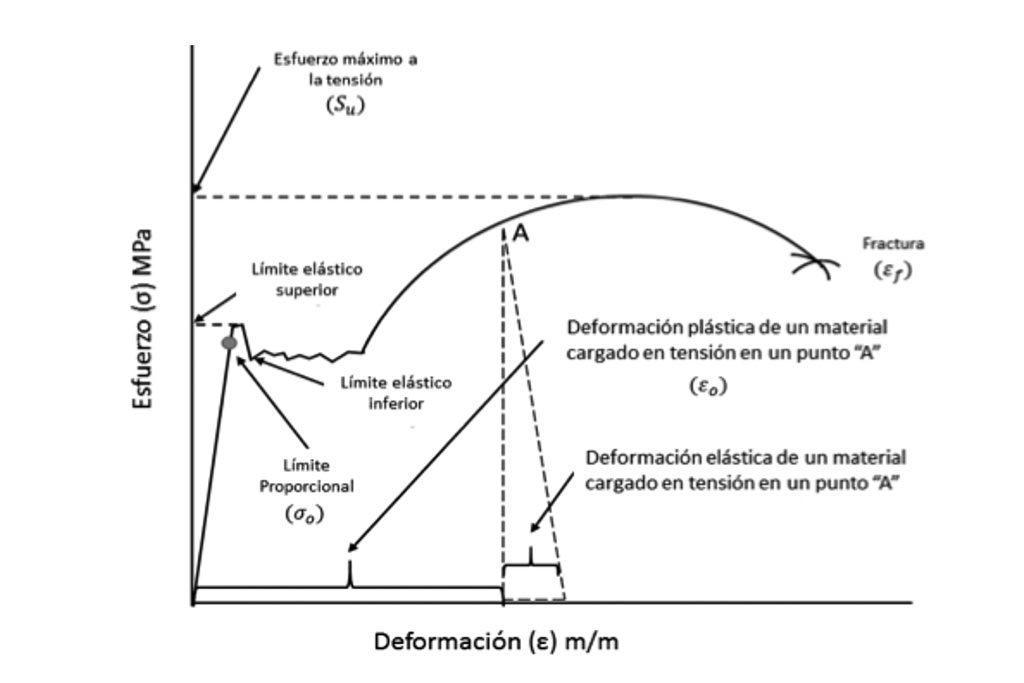
Las pruebas de tensión y compresión son utilizadas para la determinación de las propiedades de los materiales. Los procedimientos para llevar a cabo las pruebas de tensión se describen en manuales especializados y, a través del uso de las teorías en análisis de fallas, estos datos pueden usarse para predecir el fallo de piezas sometidas a esfuerzos de tensión más generalizadas. Este tipo de ensayos son considerados una buena aproximación debido a la simplicidad que conlleva la realización. Otra ventaja de este enfoque es que la condición de carga uniaxial resulta en una distribución de la tensión uniforme a través de la sección transversal de la muestra de ensayo. La curva de esfuerzo-deformación típica de la nomenclatura común se muestra en la Figura 3. En la gráfica puede apreciarse la región de deformación elástica y plástica, la cual está limitada por el parámetro σ0. Dentro de la deformación plástica ocurre el efecto de deformación permanente el cual al continuar aumentando los esfuerzos de compresión provocaran la fractura (εf).
El módulo de resistencia (Ut) es la cantidad de energía absorbida por el material durante el ensayo de compresión hasta conseguir la fractura. Este se calcula conociendo el área total bajo la curva del gráfico σ – ε (Figura 3) como se muestra en la Ecuación 3.
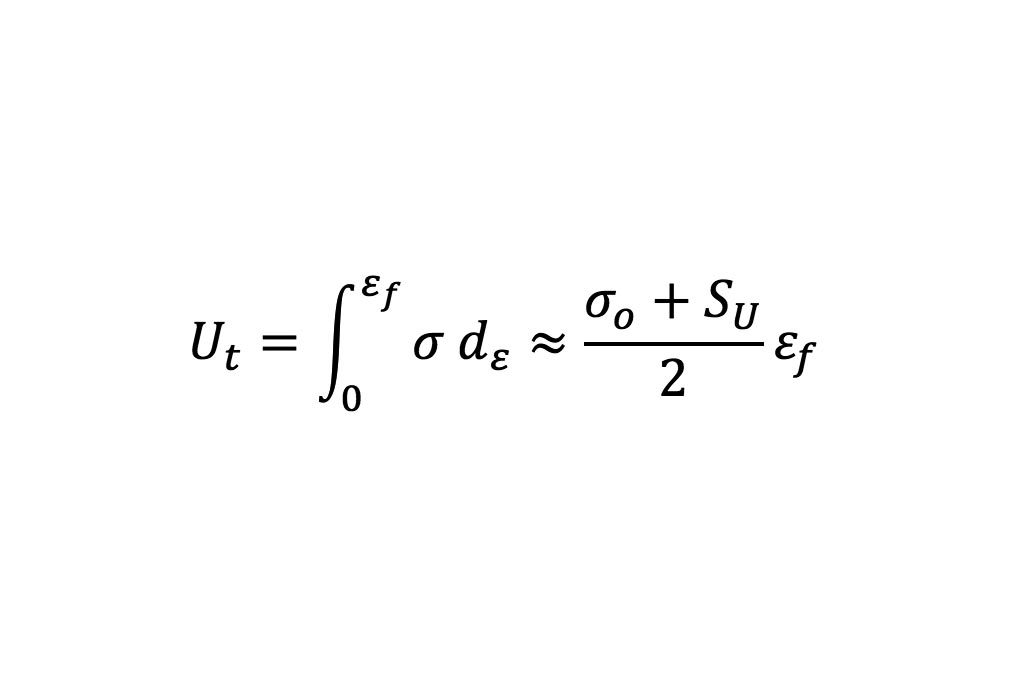
(3)
donde SU es el esfuerzo máximo a la tensión, σo se refiere al límite elástico y εf deformación a la cual ocurre la fractura. El término Ut es importante en la selección de materiales para aplicaciones en donde es probable que se produzcan sobrecargas cuando grandes cantidades de energía deben ser absorbidas (J/m3).
La Figura 4 muestra las curvas de carga para 600, 300 y 100 kN. El esfuerzo máximo a la compresión (N/mm2) y la carga máxima es posible calcularla con el área del pistón previamente conocida.
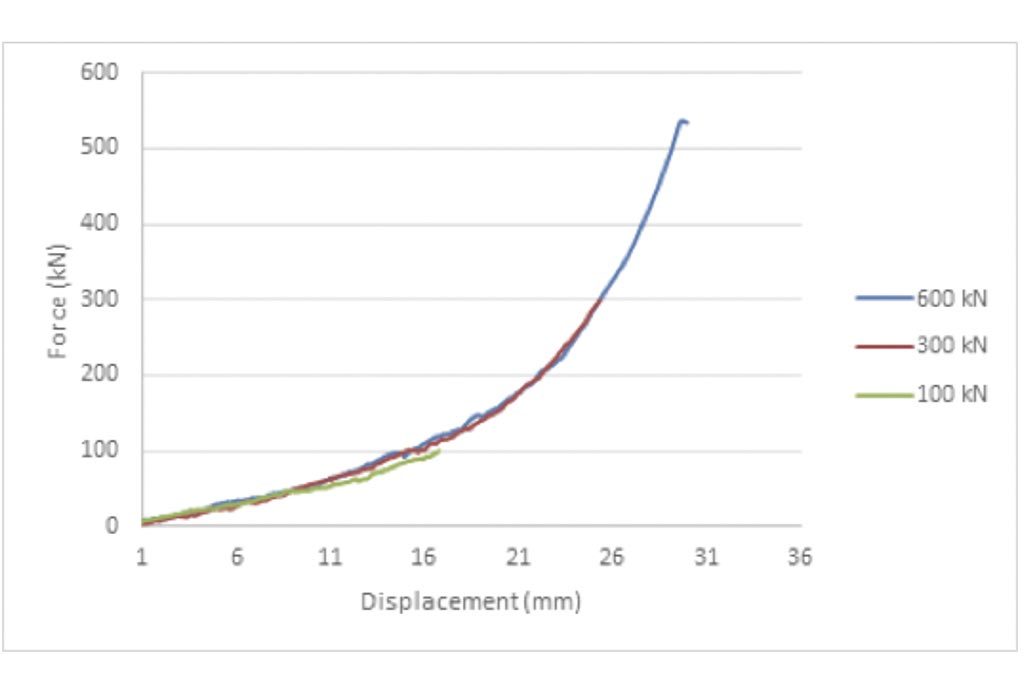
de mineral CuFeS2
Cálculo de consumo de energía específica (SPCM)
El modelo de consumo de energía específica (SPCM por sus siglas en inglés) se calcula a partir de la representación gráfica de la prueba de compresión (Figura 4), la cantidad de energía utilizada (W en Joules) se calcula utilizando una variación del módulo de dureza (Ut en J/m3) y usando el volumen interno del pistón (Vp en m3). La ecuación 4 se puede reescribir como:
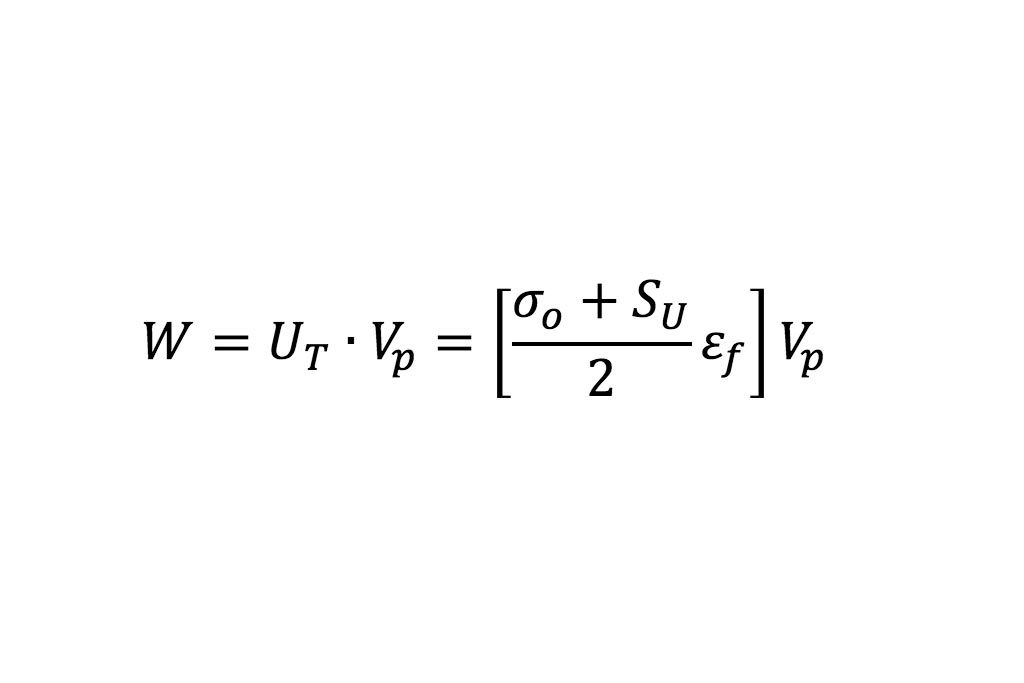
(4)
Tomando en cuenta W y T (rendimiento del equipo), la energía específica, Ee, (kWh/ton) se calcula utilizando la Ecuación 5 como sigue:
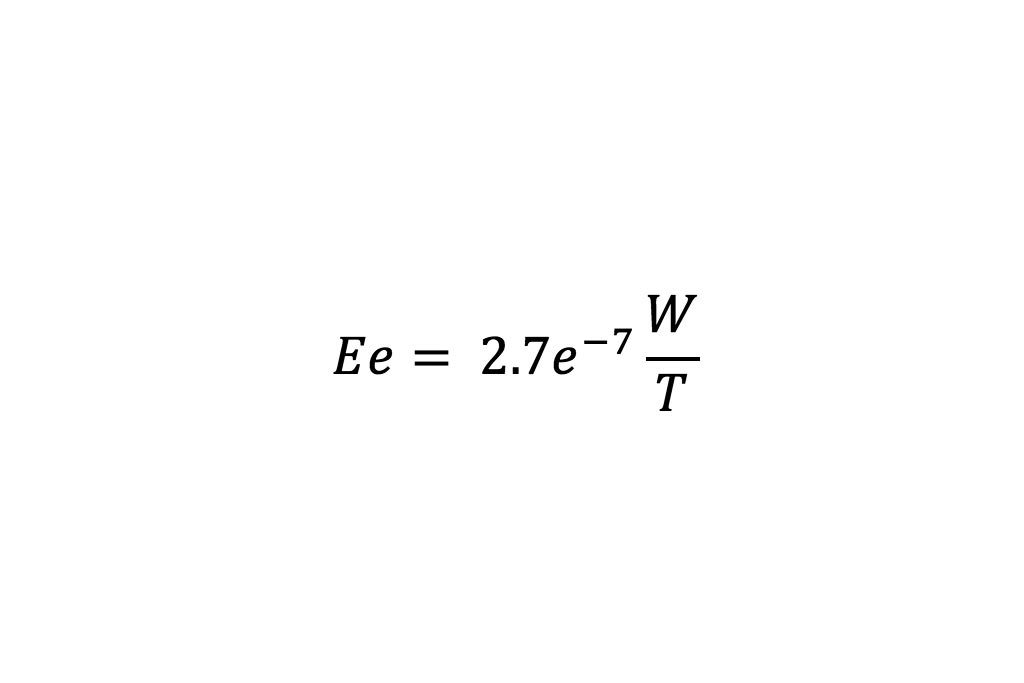
(5)
donde 2.7e-7 es el factor de conversión de Joule a kWh. Este modelo, determina la cantidad de energía utilizada durante el evento de compresión. Para determinar la granulometría obtenida en la prueba de compresión se utiliza el modelo de balance poblacional (PBM) descrito con anterioridad.
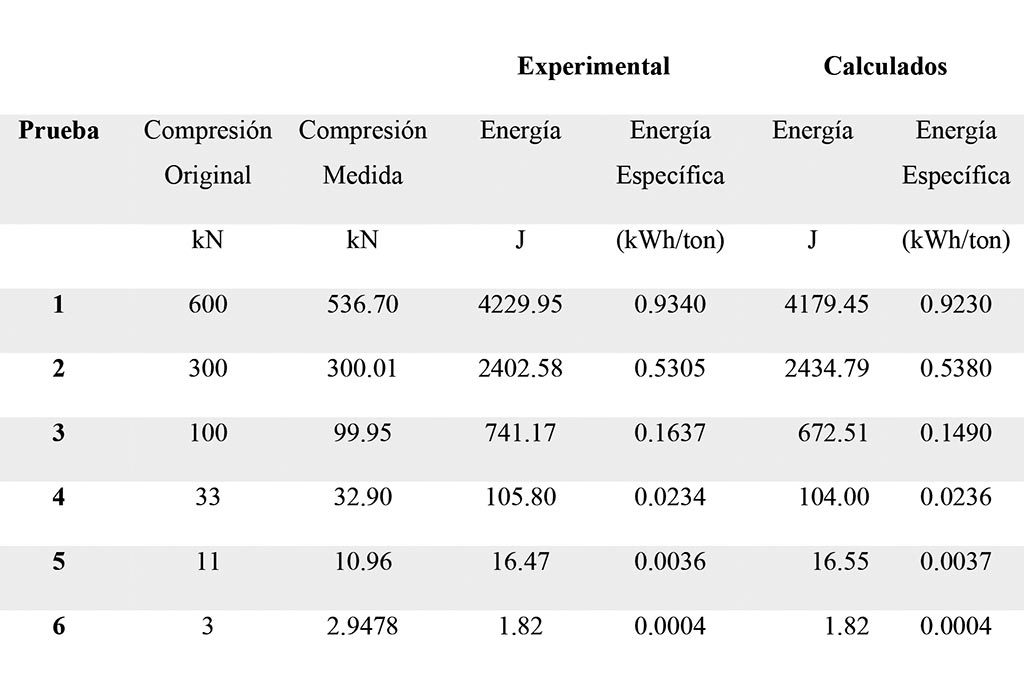
La Tabla 3 muestra la energía específica experimental frente a las energías específicas calculadas. El consumo de energía específica fue de menos de 1 kWh/ton y el modelo fue bastante preciso en esta predicción.
A continuación, en la Figura 5 se muestra la distribución de partículas generadas por la compresión de partículas.
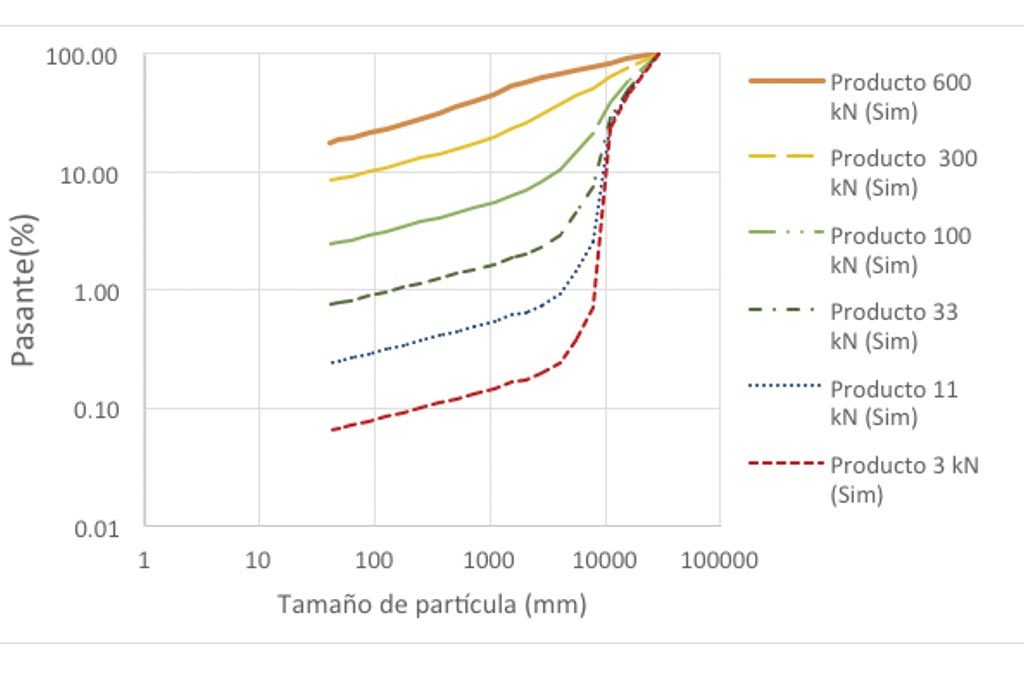
Como se puede apreciar, una distribución granulométrica donde aparecen tamaños más finos es generada. En general, los sistemas de fractura por compresión se basan esencialmente en los puntos de contacto entre las partículas, e incrementando éstas se generará una mayor fractura. Las partículas sometidas a compresión de partículas presentan un estallamiento de partículas, lo que genera partículas más pequeñas, así, estos monotamaños en colindancia con las partículas finas creadas tendrán un gran número de puntos de contacto lo que ocasionará que la fractura se genere de forma espontánea, ya que las partículas vecinas de mayor tamaño en colindancia con partículas de menor tamaño siempre aceleran la fractura.
Conclusiones
De acuerdo con los resultados obtenidos pueden concluirse los siguientes puntos.
Los resultados de los ensayos estudiados en el artículo mostraron que el consumo de energía de compresión por pistón fue menor de 1 kWh/ton y el modelo presentado en este trabajo fue preciso en dicha predicción.
El consumo de energía por compresión de partículas es considerablemente menor al de la trituración convencional. La fractura por compresión de partículas alcanza apenas 0.9340 Kwh/ton contra los 8.30 kwh/ton de la trituración, esto representa un ahorro del 94.50% de la energía usada para molienda de bolas.
Agradecimientos
Los autores agradecen a la SEP por apoyo brindado al proyecto UASLP-PTC-614, número 511-6/17-7930.
Referencias
Bulled, D., Husain, K., Lozano, C., 2009. A small-scale test to determine a work index for high pressure grinding rolls. Proceedings of the 41st Annual Canadian Mineral Processors Conference, Ottawa, Canada. pp. 86-93.
Daniel, M. J., 2002. HPGR verification and scale-up. Master of Engineering Science (research). University of Queensland. pp. 31:96-105.
Djordjevic, N., Morrison, R., 2006. Exploratory modelling of grinding pressure within a compressed particle bed. Miner. Eng. 19, 995–1004.
Fuerstenau, D. W., Gutsche, O., Kapur, P. C., 1996. Confined particle bed comminution under compressive loads. International Journal of Mineral Processing 44-45, pp. 521-537.
Hawkins, R. 2007. A piston and die test to predict laboratory-scale HPGR performance. Master of Philosophy (Engineering and Related Technology). Julius Kruttschnitt Mineral Research Centre, Dept. of Mining, Minerals and Materials Engineering, University of Queensland. pp. 60-75
Liu, R., Xiaoqian, G., Dan M.., 2014. The Mechanical Properties of Mudstone at High Temperatures: an Experimental Study., Rock Mechanics and Rock Engineering July 2014, Volume 47, Issue 4, pp 1479–1484.
Oettel, W., Husemann, K., 2004. The effect of a grinding aid on comminution of fine limestone particle beds with single compressive load. International Journal of Mineral Processing 74, pp. 239-248.
Schönert, K., 1988. A first survey of grinding with high-compression roller mills. Int. J. Miner. Process. 22, 401–412
1Coordinación Académica Región Altiplano, Universidad Autónoma de San Luis Potosí,
Carretera a Cedral km 5+600, Ejido San José de las Trojes, Matehuala, S.L.P. C.P. 78700, México
Autor de correspondencia: *(gilberto.rosales@uaslp.mx)


















